Quantitative Mineral Analysis by FTIR Spectroscopy
Zhiyong Xu,a Bahne. C. Cornilsen,b
Domenic.C. Popko,a Wayne.D. Pennington,c
James.R. Wood,c and Jiann-Yang Hwang a
aInstitute of Materials Processing,
bDepartment of Chemistry
and cDepartment of Geological Engineering and Sciences
Michigan Technological University
Houghton, MI 49931
USA
Email: zhxu [at] mtu.edu
Introduction
Traditionally, X-Ray diffraction (XRD) is used to identify minerals of oil well core samples [1]. The capability of XRD for quantitative analysis for minerals is limited to the minerals having good crystal structures. For the amorphous and low crystallite minerals, XRD cannot provide accurate quantitative information. At the same time, even for minerals with a good crystal structure, XRD measurement is a time-consuming technique.
FTIR spectroscopy is a potential alternative method for acquiring quantitative mineralogy. Infrared spectroscopy has not been utilized significantly in quantitative analysis of oil field minerals. The main uses have rather been in identification of minerals and in structural studies [2 – 4]. Typical spectra of minerals display characteristic features which can be related qualitatively to variations in the constituent minerals. FTIR spectroscopy has recently been receiving attention for its potential use in quantitative mineral analysis [1, 2, 4-10].
FTIR spectroscopy relies on detection of vibrational modes, i.e. lattice vibrations and/or molecular group vibrational modes. Mineral identification is possible because minerals have characteristic absorption bands in the mid-range of the infrared (4000 to 400 cm-1). The concentration of a mineral in a sample can be extracted from the FTIR spectrum because the absorbance of the mixture is proportional to the concentration of each mineral. This is given by Beer’s Law (equation 1), where A is the absorbance of a mineral mixture at a given wavenumber, a is the number of mineral components, e j is the absorptivity of component j, l is the absorption path length (pellet thickness), and cj is the concentration of component j. All multicomponent analyses are based on Beer’s law, and the absorbance at a specific wavenumber is the sum of the absorbance of all sample components that absorb at that wavenumber.
![]() (1)
(1)
In order to achieve the goal of accurate quantitative analysis by FTIR, meticulous and consistent sample preparation is critical. For an accurate quantitative analysis by FTIR, the particle size should not exceed 2.5 m [6]. This limit coincides with the shortest wavelength radiation used in mid-IR. When particle size is larger than or equal to the wavelength of the incident infrared radiation, there will be a decrease of the intensity of the absorption band, an increased background, broadened peak shapes, and sloped backgrounds [1].
Before the recent technological advances of computer equipment, the measurement of peak heights or peak areas was the common technique for quantitative analysis. Recently, a suite of chemometric approaches such as multiple linear regression, principal component regression, classic least-squares, partial least-squares, wavelets, and factor analysis provide more choices for quantitative analysis by FTIR [11-17]. Among these methods, least-squares fit is most widely used. Unfortunately, when using the least-squares model to fit the spectra of unknown samples with the standard matrix, the analysis can fail and negative coefficients may appear. Negative coefficients are meaningless, because it is impossible to have negative mineral concentrations. Recent work has focused on the development of a Non-Negative Least-Squares (NNLS) method for use with FTIR to overcome this limitation [6,10]. NNLS is a promising deconvolution algorithm, which is based on Non Negative Least Squares matrix inversion. This project will apply the NNLS algorithm to calculate the mineral composition of core samples.
The basis of the quantitative analysis of minerals by FTIR is the availability of a standard matrix of mineral FTIR spectra. This standard matrix is different from the common FTIR spectra of minerals, which only provide the qualitative information for identification of minerals. This standard matrix contains quantitative information for the minerals, including the absorbance at each step in the spectrum for each mineral at a given concentration in the KBr pellet (0.33 mg/300 mg KBr). Collecting the standard minerals, scanning them in a standard procedure, and normalizing the spectral data need to be done for establishing the matrix.
It is well known that in the linear region of Beer’s law, the mixture spectrum is a linear combination of the different mineral standard spectra. This combination or summation is carried out at each step or wavenumber in the spectrum, including steps or regions where there is no absorption due to vibrational modes. Such absorbance is “background.” It can be observed that this background can vary from sample to sample, independent of sample absorption. Therefore, in this study, the background has been removed to find out if its removal allows better precision or accuracy. However, in the references related to the FTIR quantitative analysis, discussion about background subtraction techniques is seldom found. In addition to removing the background, it is also possible to ignore spectral regions where there are no peaks. In this project, “the Linear Background Subtraction Procedure” (LBSP) for FTIR spectra, including omission of empty spectral regions, is developed in order to minimize the adverse effect of background.
Experimental
Spectra for 13 standard minerals, which cover the predominant minerals in oil well, were collected. These standards are illite, kaolinite, quartz, opal-A, opal-CT, oligoclase, albite, microcline, chlorite, dolomite, calcite, gypsum, and barite. FTIR spectra were collected in the mid-IR range (4000 – 400cm-1) for these 13 mineral standards, one synthetically prepared mixture for examining the accuracy of the LBSP and NNLS algorithms, one core sample (1725.6 ft) of McKittrick Front well in the Cymric Oil Field, and one core sample (2860 ft) of well KCL 44-375X in the Pioneer Oil Field.
Sample preparation for quantitative FTIR analysis is critical to the successful quantitative analysis. The typical sample to KBr ratio used is 1 mg sample/900 mg KBr. This ratio was chosen so that the absorption bands are in the linear region of Beers Law, and so that the signal-to-noise ratio is maximized. Reliable quantitative analysis of samples depends on precise and reproducible sample preparation. For an accurate quantitative analysis by FTIR, the particle size should not exceed 2.5 m . This limit coincides with the shortest wavelength radiation used in mid-IR analysis (2.5 m ). Particles that are comparable in size to the wavelength of the light interact with the light, and lead to broadened peak shapes and sloped baselines. When particle size is larger than or equal to the wavelength of the incident infrared radiation, there will be a decrease of the intensity of the absorption band and an increased background. Particle size reduction and sample preparation, therefore, are very important. Particle sizes of less than 2.5 m for all samples, both standards and oil well samples, were obtained. Sample preparation for FTIR analysis was completed using the following procedures:
- The core samples containing hydrocarbons were ground with organic solvent to remove the organic matter.
- The samples of minerals, both standards and unknowns, were ground in a puck mill with absolute ethanol for 5 minutes, and then the resulting solution was centrifuged at 750 rpm for 3 minutes to remove larger particles, above 2.5 m . The remaining suspended material in the solution was of 2.5 m particle size or less. This was confirmed by examination with the Microtrac II particle-size analyzer (Leeds & Northrup Company).
- This suspension from procedure 2) was then centrifuged at 4000 rpm for 5 minutes to collect all remaining material. The resulting powder was dried at 105ºC for 24 hours to assure that water and ethanol were expelled. The dried powder was used to make a KBr pellet for the FTIR scan.
- 900 mg KBr (IR grade, Fisher Scientific Lot 942823) were mixed with 1 mg sample and mixed for 45 seconds in a Crescent Wig-L-Bug™ (International Crystal Laboratories) in order to homogeneously distribute the sample in the KBr. The mixture was then split into three 300 mg aliquots to make three transparent KBr pellets under vacuum, and 10K psi pressure for 10 minutes.
- The samples were scanned using a Perkin-Elmer model 1600 FTIR Spectrometer. Spectra were collected in the mid-IR region (4000~400 cm-1) at 4 cm-1 resolution (2 cm-1 steps) with 16 scans. Air or a pure KBr pellet was used when scanning the reference spectrum, and all samples were scanned in KBr pellets.
The sample preparation method for the standard and unknown mineral samples is shown in Fig1.
[Figure 1 is only available as a pdf file due to the way it was supplied, if you do not have Acrobat Reader then please download it FREE-OF-CHARGE from the abode website – www.adobe.com]
Data Analysis
The Linear Background Subtraction Procedure (LBSP) for FTIR spectra was developed in this project by using an EXCEL spreadsheet macro method. First EXCEL was used to find the minimum of the absorbance in one spectrum, then adjust this minimum to zero, and adjust all the absorbances of the entire wavenumber range relative to this minimum. The other backgrounds are removed linearly. The LBSP method is demonstrated in Figure 2. The use of LBSP, together with omission of spectral regions containing no sample absorbance, is expected to improve the results of FTIR quantitative analysis of minerals.
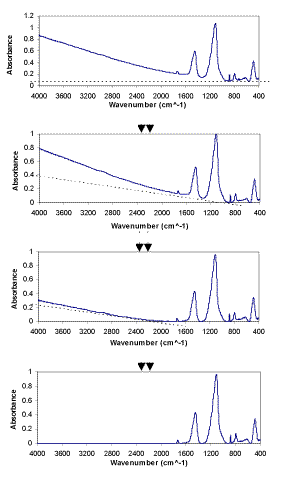
Figure 2. The linear background subtraction procedure (LBSP) of FTIR spectra
Non-Negative Least Squares (NNLS) is an algorithm (equation 2) that solves a matrix of linear equations (equation 3) with non-negative constraints. This is a quite straightforward application of a complicated preexisting constrained linear algebra algorithm and was first developed by Lawson and Hanson [18]. Matlab™ is used to solve this deconvolution algorithm, based on a NNLS matrix inversion. It implements the matrix calculation algorithm, xj = NNLS (Aij, bi), to allow NNLS to deal with a very huge amount of data in a short running time. Aij is the standard spectral matrix (containing absorbances for a minerals and ß data points) of standard minerals (see equation 4). xj is a vector with concentrations of a different minerals in the unknown sample, and bi is the spectrum absorbance vector (containing ß data points) for the unknown mixture.
Aij * xj = bi, (2)
![]() (3)
(3)
Therefore, equation 2 is solved for each spectral data point (bi) in a least squares sense, subject to the constraint that the solution vector x has non-negative elements xj ³ 0, j =1, 2, … a . Values for xj are calculated to fit the observed bi values using equation 5.
All the FTIR spectra were collected with 4 cm-1 resolution. Therefore, with 2 cm-1 steps there are a total of 1801 data points (ß) for each spectrum from 4000 to 400 cm-1. Then according to Beer’s law, the quantitative analysis for a mineral requires solution of 1801 equations (for the 1801 data points in each spectrum) to obtain the 13 unknown concentrations xj (j= 1, 2, …a, where a = 13 for 13 standards).
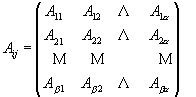 (4)
(4)
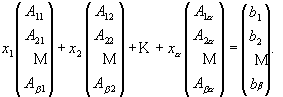 (5)
(5)
Click here to view pdf files of equations 4 and 5
Results & Discussion
The mineral standards include 13 minerals: illite, kaolinite, quartz, opal-A, opal-CT, oligoclase, albite, microcline, chlorite, dolomite, calcite, gypsum, and barite. They have been carefully selected and examined using SEM, ICP, and XRD analytical techniques. The FTIR absorption spectra of the thirteen mineral standards were obtained. The spectrum of one synthetic mixture is obtained and the calculated result (with or without background removal and for different wavenumber ranges) is listed and compared to the weighed amounts (Table 1).
| MINERAL STANDARDS | ACTUAL | Calculated (MATLAB) | ||||
| before substraction |
after substraction* |
|||||
| 4000-400 | 4000-400 | 1600-400 | ||||
| SHEET SILICATES |
CLAYS | Illite | ||||
| Kaolinite | 0.30 | 0.32 | 0.27 | |||
| CHLORITE | Chlorite | 0.29 | ||||
| FRAMEWORK SILICATES | SILICAS | Quartz | 0.30 | 0.11 | 0.28 | 0.28 |
| Opal-CT | ||||||
| Opal-A | 0.09 | |||||
| FELDSPARS | Oligoclase | 0.17 | ||||
| Albite | ||||||
| Microcline | ||||||
| CARBONATES | Dolomite | 0.29 | ||||
| Calcite | 0.40 | 0.40 | 0.40 | |||
| SULPHATES | Gypsum | 0.06 | ||||
| Barite | ||||||
Weighed (actual) and calculated composition (wt.fraction) for synthetical mixture.
* Area under background is removed with LBSP (Linear Background Subtraction Procedure) as defined in Figure 2.
Table 1.
The mineral percentage of the synthetic mixture is first calculated “without background removal.” The result is not in good agreement with “actual” weighed amounts (see Table 1, 4000-400 cm-1, “before subtraction”). The disagreement is very large, and the specific minerals are not distinguished.
To determine how the non-zero and variable backgrounds influence the calculated percentages, we compare calculated compositions using spectra with a non-zero background with those calculated using spectra which have had the background removed (see Table 1, 4000-400 cm-1). The calculated percentage “after background subtraction” using the LBSP are in good agreement with the actual percentages (within 2 to 3%). This is much better accuracy than in the previous analyses. Furthermore, the individual minerals have been distinguished. Therefore, application of the LBSP procedure to remove all background gives a better (i.e. more accurate) quantitative analysis.
For the results calculated after LBSP, two different regions (4000-400 cm-1, and 1600-400 cm-1) are also compared in Table 1. The results for these two regions are very similar. The accuracy can be improved by eliminating the background. Omitting the 4000-1600 cm-1 spectral region does not significantly improve the results any further. Values for a third region (the combination of 4000-3000 cm-1 and 1600-400 cm-1 after subtraction) were also calculated. These are not included here because these are similar to those for the 1600-400 cm-1 region.
The experimental FTIR spectra and calculated spectra (using LBSP and NNLS algorithms) for one sample (2860 ft) from well KCL 44-375X in the Pioneer Oil Field, and one sample (1725.6 ft) from McKittrick Front well #418 in the Cymric Oil Field, in Kern County, CA, USA, are shown in Figures 3 and 4. For these two samples, the LBSP and the 1600-400 cm-1 region have been used for FTIR quantitative analyses. The mineralogical analyses for these two samples are shown in Table 2. Visual inspection of the two spectra in each figure allows one to see where the fits are better and where they are not so close to each other. Table 2 demonstrates that the calculated data agree very well with the experimental data.
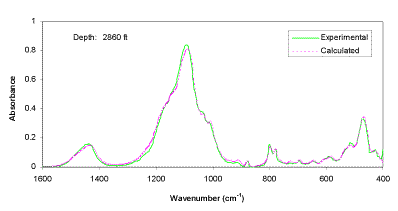
Figure 3. Comparison of experimental and calculated FTIR spectra for well KCL 44-375X, in the Pioneer Field, Kern Country, CA, USA.
pdf file available
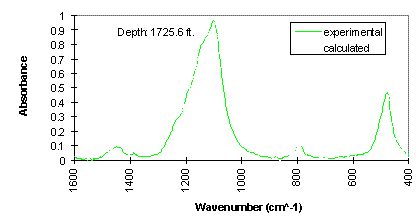
Figure 4. Comparison of experimental and calculated FTIR spectra for McKittrick Front well #418, in the Cymric Field, Kern County, CA, USA.
pdf file available .
| Minerals | McKittrick 1725.6 ft. | Pioneer 2860 ft. |
| ALBITE BARITE CALCITE CHLORITE DOLOMITE GYPSUM ILLITE KAOLINITE MICROCLINE OLIGOCLASE OPAL-A OPAL-CT QUARTZ |
0.0 0.0 0.0 4.8 6.1 6.6 0.0 1.2 0.0 0.0 0.0 81.4 0.0 |
0.0 0.0 6.5 0.0 4.6 0.7 3.5 10.6 12.8 6.7 0.0 26.7 27.8 |
Table 2. The FTIR mineralogical analyses (wt%) for McKittrick Front well #418, in the Cymric Field and well KCL 44-375X in the Pioneer Field, Kern County, CA, USA.
In order to examine the accuracy of the FTIR quantitative analysis for a core sample, the powder X-ray Diffraction (XRD) patterns were also obtained for these two samples [19]. Then area fit software was used to fit the XRD patterns for opal-CT and quartz peaks, and the ratio of opal-CT and quartz was obtained [19]. The comparison of results from FTIR analysis and this XRD fit are shown in Table 3. In the Pioneer 2860 ft sample, for opal-CT, the result is 49.0% by FTIR analysis and 49.1% by XRD peak area fit. For quartz, the result is 51.0% by FTIR analysis and 50.9% by XRD peak area fit. These also are in excellent agreement. In the McKittrick 1725.6 ft sample, FTIR does not observe any quartz, but the XRD measurement shows 2.5% quartz. XRD is expected to be most sensitive to the most crystalline phase and less sensitive to the less crystalline phases. If it underestimates the opal-CT, the quartz content can be exaggerated. Most importantly, these results obtained by FTIR and XRD are completely consistent within the experimental precision of these two measurements, which at best is ± 1 to ± 2%. This agreement substantiates the successful application of FTIR for these analyses.
| Percentage relative to total SiO2 | ||||
| McKittrick 1725.6 ft. | Pioneer 2860 ft. | |||
| opal-CT | quartz | opal-CT | quartz | |
| FTIR | 100.0 | 0.0 | 49.4 | 50.6 |
| XRD | 97.5 | 2.5 | 49.1 | 50-9 |
Table 3. Comparison of SiO2 results by using FTIR and XRD
Conclusions
Using 13 mineral standards in a “standard mineral matrix” and the Matlab™ NNLS function, the composition of unknown mineral has been determined rapidly and accurately using FTIR spectroscopy. The standard minerals were selected to represent those in the cores, and characterized by SEM, ICP, and XRD analytical techniques. Using the synthetically prepared mixture, removal of background using a “linear background subtraction procedure” (LBSP) is shown to substantially improve the analyses, i.e. improve agreement with the specific minerals and weighed amounts. Without background removal the agreement is not acceptable. However, with the LBSP, agreement is good to ± 2%. Therefore, removing the background of a spectrum is a key factor for successful quantitative analysis. The LBSP is then applied to analyze oil well core samples. Two samples were analyzed. These results demonstrate the power and potential of FTIR spectroscopy for quantitative mineral analysis. The FTIR spectroscopic method is superior to XRD because it is sensitive to amorphous, as well crystalline phases.
References
- B. H. Ruessink and D. G. Harville, Paper SPE 23828, SPE International Symposium on Formation Damage Control, Lafayette, Louisiana, 1992, pp. 533-546.
- Z. Xu, XAS and XRD Structural Study of Nickel Electrode Materials (Part I) and FTIR Quantitative Analysis of Mineral Mixtures (Part II), PhD Dissertation, Michigan Technological University, Houghton, MI, 1999.
- V. C. Farmer (ed.), The Infrared Spectra of Minerals, Mineralogical Society, London, 1974.
- D. M. Moore and R. C. Reynolds, X-ray Diffraction and the Identification and Analysis of Clay Minerals, Oxford University Press, New York, 1989.
- T. L.Hughes, C. M. Methven, T. G. J. Jones, S. E. Pelham, P. Eletcher, and C. Hall, Advanced Cement Based Materials, 2, 91-104 (1995).
- A. Matterson and M. M. Herron, Paper # 9308, Society of Core Analysis Conference, 1993.
- D. G. Harville and D. L. Freeman, Paper SPE 18120, The 63rd Annual Technical Conference and Exhibition of the Society of Petroleum Engineers, Houston, TX, 1988, pp. 141-150.
- P. C. Painter, S. M. Rimmer, R. W. Snyder, and A. Davis, Applied Spectroscopy, 35, 102-106 (1981).
- R. W. Synder, P. C. Painter, and D. C. Cronauer, Fuel, 62, 1205-1214 (1983).
- A. Matteson and M. M. Herron, Journal of Sedimentary Petrology, 63, 1133-1148 (1993).
- P. Saarinen and J. Kauppinen, Applied Spectroscopy, 45, 953-963 (1991).
- D. W. T. Griffith, Applied Spectroscopy, 50, 59-70 (1996).
- P. B. Stark, M. M. Herron, and A. Matteson, Applied Spectroscopy, 47, 1820-1829 (1993).
- M. K. Antoon, J. H. Koenig, and J. L. Koenig, Applied Spectroscopy, 31, 518-524 (1981).
- P. M. Fredericks, J. B. Lee, P. R. Osborn, and D. A. J. Swinkels, Applied Spectroscopy, 39, 303-310 (1985).
- P. M. Fredericks, J. B. Lee, P. R. Osborn, and D. A. J. Swinkels, Applied Spectroscopy, 39, 311-316 (1985).
- K. R. Beebe and B. R. Kowalski, Analytical Chemistry, 59, 1007A-1017A (1987).
- C. L. Lawson and R. J. Hanson, Solving Least Squares Problems, Prentice-Hall, New Jersey, 1974, pp. 158-179.
- D. C. Popko, Quantitative Mineral Characterization of the OpalA-OpalCT-Quartz transition in the Pioneer and McKittrick Oil Fields by FTIR, XRD, SEM, and ICP, M.S. Thesis, Michigan Technological University, Houghton, MI, 1999.
REF: Z. Xu, B.C. Cornilsen, D.C. Popko,W.D. Pennington, J.R. Wood & J-Y Wang, Int. J. Vib. Spect., [www.irdg.org/ijvs] 5, 1, 4 (2001)

