Infrared & Raman Spectra of solids. Why are they different from solutions?
Patrick Hendra
Editor
A few weeks ago, a colleague asked me to explain why two bands appeared in a spectrum of a solid, where he expected only one. I duly replied by FAX but I thought that perhaps my scribbled reply, duly edited and expanded, might be useful.
As we all know – molecules containing ‘n’ atoms do so in a set of well defined ways of numbers 3n – 6 where the molecule is non-linear and 3n – 5 if linear. We also know that these modes may give rise to infrared or Raman bands. If the molecule is centro-symmetric, no mode will occur in BOTH spectra but if not centro-symmetric, some modes will show dual activity. Further, a few modes will appear in neither spectrum.
To predict something of the characteristics of a mode and its activity (IR or Raman) one defines the symmetry properties of the molecule and hence it’s point group. Armed with a set of character tables the activity of each mode can be deduced. All of this is very true and it works well for molecules in the liquid or solution phases. For gases – no problem, but quantised rotation is allowed and this in turn leads to complications [I have discussed the infrared and Raman spectra of gases recently in IJVS [www.irdg.org/ijvs] 5, 4, 3 (2001)]
Vibrations in Solids
Several important points need making before we start because the vast majority of spectra we record are on solids, most of which are crystalline.
- Spectra of crystals are almost always sharper than those of melts or solutions.
- Spectra of solids when compared to those of the solute in solution or their melts are invariably much more complex. To put it another way – comparing the spectrum of a liquid with its frozen solid, the latter have many more bands.
- The frequencies of the bands in the solid are shifted from those of itself in the liquid phase. Some bands can move considerably (30cm-1 is not unusual).
Let us now deal with the reasons in turn.
- & 3. A molecule in solution or in the liquid phase is in a state of incredibly violent translation. Adjacent molecules continuously batter it, the violence increasing as the temperature rises. As a result, the intermolecular forces are random and very variable indeed. Intermolecular forces shift the frequencies of intra-molecular vibrations hence the randomness and violence of the collisions broaden the bands [the phenomenon is similar to pressure broadening in gases]. In crystals, each molecule lies in a precise site within an overall highly regular structure. It is surrounded in 3 dimensions by other molecules
As a result all the vibrators are similar in that they are exposed to the same intermolecular force field and hence they all vibrate similarly producing sharp spectra.
In a crystal, the number of vibrations equals 3n1– 6, where n1 is the number of atoms IN THE UNIT CELL. So, in a 10-atom molecule, one expects 24 modes in its melt, but if the unit cell contains 4 molecules, the number rises to 114. Further, the infrared and Raman activity is governed by the symmetry of the unit cell NOT that of the isolated molecule. Almost invariably, the symmetry of the unit cell is similar to or lower than that of the molecule.
It is perfectly possible to carry out a full and detailed analysis of the vibrational spectrum of a crystal (or at least a simple system such as CaCO3 or other simple ionics) but it is rarely done. In more complex molecular systems it is normal to follow changes in the spectra due to phase by adopting a rather crude but useful stepwise process.
Crystal or Davydov Splitting
Let us consider a molecule, which is fairly highly symmetric and fortuitously crystallises with only 2 molecules per unit cell. Such an example is polyethylene. In polyethylene, the structure of the molecular is of class d2h, i.e. it is centro-symmetric with a good spread of planes of symmetry. Unusually, the crystal, which contains 2 molecules is also of symmetry class D2h [We are below using lower case for the molecule and upper for the crystal] i.e. the molecule and crystal are isomorphic. The structure looks like
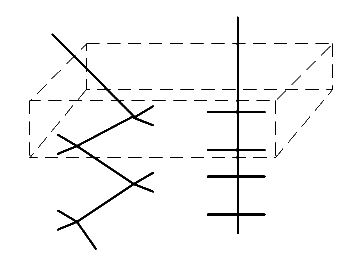
The planes through the zig-zag of carbon atoms is twisted by about 90º in adjacent molecules within the unit cell.
Let us consider just one vibration of the molecule – the symmetric C-H stretching mode
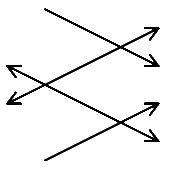
In the molecule this will generate a Raman band but no infrared mode because the molecule is d2h and centro-symmetric. In the D2h crystal there are two possibilities
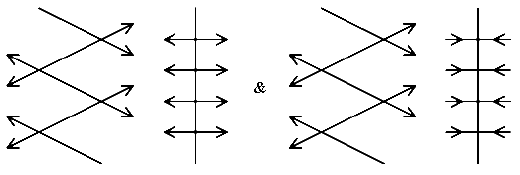
the vibrations of each molecule can be in-phase or out-of-phase with respect to its neighbour in the unit cell. Obviously, the intermolecular effects in each mode are different and as a result, the frequencies will differ and hence we MIGHT see two bands rather than one. As it turns out, the effect of the phase splits the isolated molecule frequencies by 0 to 12 cm-1.
In polyethylene, as I have emphasised, the unit cell and the molecule are isomorphous hence each mode of the isolated molecule splits into two modes of similar activity to its parent. So the Raman bands in polyethylene and also the infrared ones are seen as doublets e.g., the CH2 wag (isolated molecule ~725 cm-1) shows as an infrared doublet at 719 and 730 cm-1. The intensity of the bands is dissimilar but both crystal CH2 wags are IR active. Similarly, the Raman band at 1295 due to the twist of the CH2 shows up at low temperatures as a very close doublet.
If the molecule and the crystal are not isomorphous (and they rarely are) the Raman bands in the isolated molecule may (in fact usually do) have different activities in the crystal. Similarly the infrared active modes.
So we might have
In this hypothetical case 4 modes are generated from each isolated molecular mode. The IR active one happens to be well split, the Raman one is not. The crystal modes are split 2 x IR and 2 x R but in the Raman mode in the isolated molecule no resolution occurs.
Lattice modes
As we have seen, the number of modes in a crystal equal 3n1 – 6 where n1= the number of atoms in the unit cell. Not all of these will be intra-molecular modes, a few will result from the molecules moving as masses between themselves within the lattice. These will be, of course, low frequency (almost always below 400 cm-1 and often below 100 cm-1) and depend for their frequency on the mass of the molecule and the strength of the intermolecular force field. These modes are called ‘lattice modes’.
Infrared folk tend to ignore these because they occur below the lower limit of their routine scans (4000-400 cm-1) but Raman enthusiasts see them all the time. They can be very confusing because nothing tells the poor old spectroscopist that they are lattice modes and he/she can well misidentify them as analytically useful features.
Experimental ruses
Although it is rare to want to carry out a complete crystal analysis, some idea of the behaviour of the crystal as a vibrator is useful in some cases and can be crucial in the study of polymorphs.
Clearly, one can in principle record the spectrum of the melt or solution and compare it with the powder. Fine, but not always possible. Several snags may arise including
sample decomposes if melted and kept hot for too long.
sample doesn’t melt at all.
sample insoluble or only sparingly so.
sample is fluorescent hence Raman must be recorded on an F-T instrument. Very difficult to record spectra above 200ºC.
etc etc.
Clues as to behaviour can be deduced by using some experimental tricks.
Cooling the sample
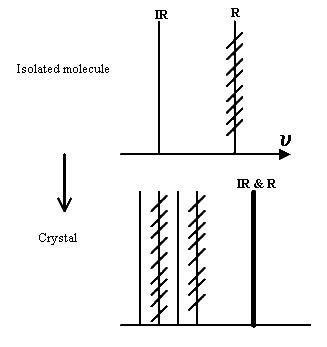
Cooling a sample tends to narrow the spectral line width. It also contracts the lattice increasing the intermolecular force field and hence increasing the splitting. Hence we might observe –
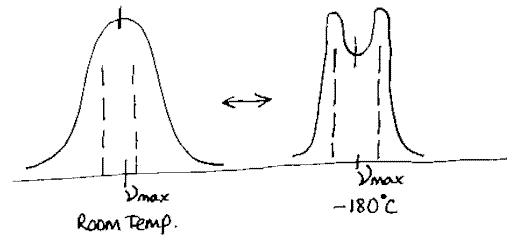
The splitting increases and the line width falls as the temperature falls. Applying high pressure increases the splitting but doesn’t narrow the line-width.
Using polarised light
The components of the crystal spectrum may well be more or less dichroic than each other each other hence, if the sample is oriented (e.g., a polymer film or a mineral wafer) the band intensities will change e.g.,
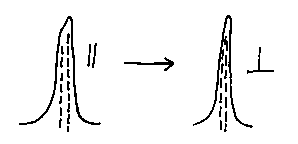
The two components responded differently to the orientation.
Sometimes, one cannot see any change in the band shape or intensity (due to the lack of splitting and/or the bandwidth) but the band head WILL shift if only by a minute amount. Data subtraction will then yield the evidence.
The use of polarised light and an analyser in the Raman tends to be more useful than in the IR. I have discussed this matter before see IJVS [www.irdg.org/ijvs] 3, 1, 6 (1999) and also Neil Everall IJVS [www.irdg.org/ijvs] 3, 2, 2 (1999).
Identifying lattice modes
Lowering the temperature does not effect the average frequency of the bands in a crystal due to internal molecular vibrations i.e. vmax above doesn’t vary. Lowering the temperature usually (almost always) shrinks the lattice and so the lattice modes usually rise in frequency. So, if a low frequency band rises in frequency as the sample is cooled, you can bet good money on it being due to a lattice mode.
Editor
REF: P.J. Hendra, Int. J. Vib. Spect., [www.irdg.org/ijvs] 6, 3, 3 (2002)

