How FTIR works III
The Editor & Fabrice Birembaut*
*University of Southampton
Highfield, Southampton
SO17 1BJ
UK
In this piece we explore some of the problems you may encounter and how to deal with them. You, the readers – have prompted one or two areas, thanks for the ideas.
The finite slit width effect
We have touched on this subject before but more detail is required. Back in the days of infrared spectrometers based on scanning mono-chromators, the effect of the slit-width on the spectrum was recognised. Let’s assume the spectral feature you want to examine is very, very sharp (say a w½ value of 0.1cm-1). The slit width is set at a wider width c x dispersion = 1cm-1 or if you prefer, the bandpass is 1cm-1. As the mono-chromator scans the image of the entrance slit across the open jaws of the exit slit we see
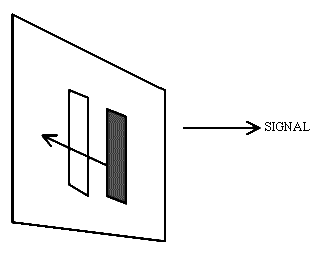
and the magnitude of the signal at the detector is
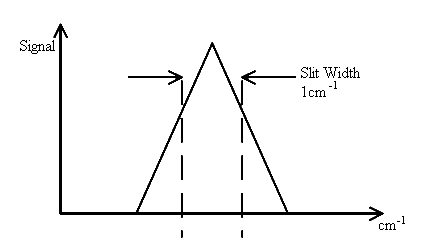
Thus, a spectral feature of width 0.1cm-1 appears as a band with a half width of 1 cm-1. To correct this problem the slit width must be narrowed to less than 0.1cm-1. This may well be possible, but the quality of the optics and mechanical drive may not permit you to do so efficiently. However, narrow the entrance slit, there will be a minimum width of image. Optical imperfections could well be such that the lower limit is ½cm-1 so very narrow features (e.g., gas phase spectra) are simply not accessible without distortion. Now – what happens with an interferometer.
In a sense, the same thing – there is a limit to the quality of the optics and this defines the smallest value of the J stop you can usefully use. As the resolution is improved, you have to use a smaller J stop, so quite clearly for any given instrument its quality will define the limit of resolution available. In addition, as we have explained before, as you wish to improve the resolution, you must acquire more data points i.e. you must increase the length of the mirror scan. A path difference scan of 1cm will satisfy a need for 1 cm-1 resolution but a huge 10cm movement is needed if you want 0.1cm-1 resolution – not easy to do without shake or wobble hence the cost of high resolution instruments.
All of this is academic if you habitually look at solids because the bands are broad – BUT IS IT? Assuming you are careful to keep the resolution better than the narrowest band in the spectrum, all seems well but not quite – there is the problem of the S:N ratio.
Returning to the old spectrometers. The amount of energy that passed through the mono-chromators was proportional to the (slit-width)2 so using very narrow slits could be a bit of a disaster. In interferometers, the energy that goes through the instrument is also proportional to the size of the J stop squared.
This might seem a little odd because only one J stop is fitted – the entrance one – the manufacturers leave out the exit aperture and hence the exit J stop is virtual to use optical parlance. Whether virtual or not, the exit J stop acts as if it were there because the detector has a limited size.
Be that as it may, higher resolution = noisier spectra requiring that you co-add more scans.
Again, as we have explained before, if the resolution is too low bands will appear broader than they should be but the area under the band is not effected by the resolution. Several of the points above are explained in Table 1.
| Fixed J stop: 8.17mm | ||||
| Resolution | Peak Height | Area | Width | Centre |
| 1cm-1 | 278.77 | 1577.6 | 4.4643 | 988.52 |
| 2cm-1 | 260.18 | 1560.5 | 4.7772 | 989.23 |
| 4cm-1 | 218.96 | 1575.9 | 5.9274 | 989.23 |
| 8cm-1 | 85.178 | 1490.9 | 16.44 | 989.12 |
| Fixed resolution @4cm-1 | ||||
| J stop | Peak Height | Area | Width | Centre |
| 4.09mm | 51.358 | 324.84 | 5.1546 | 989.03 |
| 5.78mm | 124.69 | 821.61 | 5.3339 | 989.23 |
| 8.17mm | 216.85 | 1555.2 | 5.9104 | 989.21 |
| 11.55mm | 242.18 | 2009.5 | 6.9059 | 988.06 |
| 12.50mm | 241.22 | 2041.2 | 6.9996 | 987.47 |
Table 1. Barium Sulphate results
In Raman spectroscopy, bands tend to be very narrow so we used an FTIR in its Raman mode to demonstrate. The sample was BaSO4 and the sharp clear band at 989cm-1 was our model. See Figure 1.
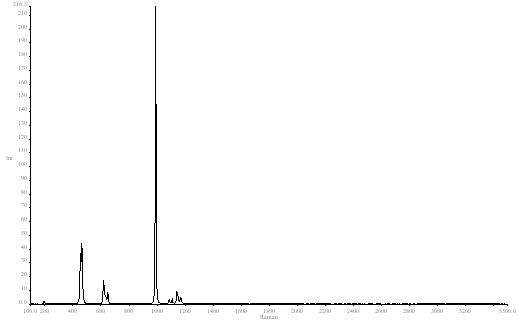
Figure 1. Barium sulphate spectrum
In the first block of data the J stop was fixed at 8.17mm width. As the spectra were run at ever decreasing resolutions 1cm-1 16cm-1 the peak fell in height but not in area. The width of the band increased as expected. See Spectrum 2 The actual fundamental bandwidth of this feature in BaSO4 is about 4 cm-1 , so the band has a limiting lower width or around 4 cm-1 however fine the resolution.
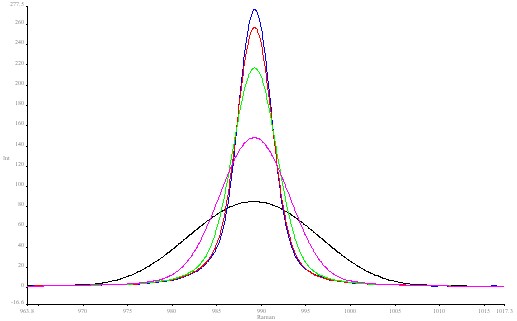
Figure 2. Barium sulphate spectrum using various resolutions:
blue 1 cm-1; red 2 cm-1; green 4 cm-1; pink 8 cm-1; black 16 cm-1.
In the lower block of data (see Figure 3) the resolution is fixed at the optimum value (4cm-1), but the J stop size is varied over a range of 3:1. Several interesting points arise. As you increase the J stop more energy passes through the instrument the amount varying as the J stop diameter increases but not linearly – it tails off at larger values.
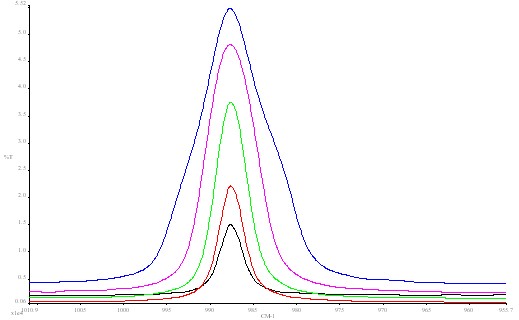
Figure 3. Barium sulphate spectrum using different J stop values:
blue 4.09 mm; red 5.78 mm; green 8.17 mm;
pink 11.55 mm; black 12.50 mm.
This is because the image of the imaginary exit J stop over fills the detector at large J stop values which has a delimited size (in this case ~1mm square).
To summarise: always try to use a resolution better than the sharpest line in the spectrum but only just better. For quantitative work only use the peak heights if you are certain that you have satisfied the first condition. If not always use the band areas.
A word of caution: Over the years the Southampton group have experimented widely with the use of band heights and areas in quantitative analyses (almost exclusively in Raman, but the principles apply equally to FTIR). We almost invariably found that peak heights are a more accurate measure of quantity than areas. Why? We think the reason is that the background is hard to precisely define. When measuring areas a small variation in the background height has an enormous effect on the integrated area for obvious reasons, but has little effect on the measured band height.
Note on Spectrographic Instruments
All the above discussion refers to FT instruments. These days much of the Raman work done is carried out on spectrograph CCD detector microscope instruments. Some of the points still apply. In Table 2 we give some data recorded on a Renishaw Microscope Raman System.
| Slit Width |
Band Area | W½ | Peak Height |
| 20 | 57 | ~4 | 15 |
| 40 | 109 | 4 | 22 |
| 80 | 227 | 4 | 37 |
| 160 | 420 | 6 | 48 |
| 320µ | 735 | 9cm-1 | 50K counts |
Table 2.

Figure 4. Barium sulphate spectra recorded using various slit width:
black 20 um; Red 40 um; Green 80 um; Pink 160 um; Blue 320 um.
The sample was again BaSO4 and the target band, the one at 988 cm-1. Clearly, there is little point in this case in using a slit width less than 80 µ. Further note that the band area rises as the slit width NOT the slit width2. This is because the array type CCD detector ‘sees’ the image of the slit in its entirety and the peak height is the signal on the most brightly illuminated pixel. As a further consequence, the peak height rises at the power less than (slit width)1.
Way back in the past, when doing quantitative work, the use of peak heights was almost universal and it was accepted that the instrument response would be quirky and non-linear. As a result, calibration curves on a wide range of carefully prepared standards were always calculated and then used on unknowns. The quantities were read off the calibration curve. These days there is a tendency to check for linearity using a few samples and then let the computer calculate the quantity automatically. For good work a little humility and caution is indicated. Assume your methods are suspect, try various combinations of measurement method and calibration routine use the best and don’t overestimate the accuracy with which you claim your analyses – particularly at high and low concentrations.
Frequency accuracy
As the venerable American economist Prof. John Kenneth Galbraith always insists, the study of economics is frequently dominated by myths so the same is true in our field – the myth of frequency accuracy.
Some manufacturers mutter that because the measurement of the optical delay is measured using a helium neon laser, the measurement is limited in accuracy only by our knowledge of the He/Ne wavelength and as an inevitable consequence, the position of the bands in an FTIR are precise. End of Story. Well its not the end.
The argument above would be valid if the measurement of the fringes as they fall on the fringe detector was perfectly precise, but of course it is not. This error although present is insignificant compared with the problem of uneven J stop illumination.
The path difference through the interferometer is defined as that along the optical axis but a cone of rays whose cone angle is defined by the size of the J stop in fact passes through the instrument. If the cone is symmetrical about the optic axis, the average optical delay will equal the measured one.
Let us assume that you are using an accessory (say a diamond ATR) or a small volume transmission cell or any microscope, the chances that the cone of rays passing through the interferometer will be precisely centred on the optic axis is zero. As a result, the measured delay is erroneous and the bands in the spectrum will be shifted.
Does the effect appear as a real problem?
In Figure 5, we show FT Raman spectra of potassium permanganate. [We use Raman again here because it is easy to misalign the experiment in the Raman. In using FTIR accessories it happens by inevitable accident and is impossible to control].

Figure 5. Raman spectra of a KMnO4 crystal.
Red is best position; green is right shifted and blue is left shifted.
The spectra demonstrate the point nicely. Using 4cm-1 resolution we looked at a crystal found the ‘best’ position and then misaligned so that the signal strength fell by 50% to one side and then the other. As you can see, the band shifts but not by the same amount each side. The shift is small but can in many cases exceed a wavenumber. Some physico chemical experiments rely on band head shifting (with temperature, pressure applied stress, concentration etc, etc.) and often the shift range is only a few cm-1. The myth that FTIR (and FT Raman) are inherently accurate leads people to assume that they can make measurement of significance to shift values down to ¼cm-1 or less – MAYBE.
The instrumental shift depends on misalignment so in making these measurements you must guarantee that the misalignment remains constant throughout the experiment e.g., using a small volume liquid cell take precautions that the cell is located in the sample area reproducibly as each spectrum is recorded and check using repeat runs that this is so. Similarly with ATR, but be very, very careful when using inhomogeneous samples – Many years ago I remember we ran the first Raman spectrum of polyacrylonitrile fibre using the then novel FT Raman machine at Southampton. Careful scrutiny showed that the dyed and undyed uCN bands were at different frequencies. We could see the interaction of the dye and the fibre. A note was hurriedly prepared – ‘t would be the note of the year! Fortunately, the next day Henry Mould visited us from Perkin Elmer, UK. He looked at the spectra, tugged his chin and suggested we bin the paper. He then explained the myth described above. The laser illuminating the bundle of fibres quite obviously generated an uneven patch of Raman scatter at the J stop and this would vary from sample to sample. Such was our wonderful earth shattering discovery.
Deconvolution process
To finish this piece we decided to look at the band deconvolution process. The questions are: “how reliable are my results?”, “which output should I chose?”, “how many peaks should I use when deconvoluting my bands?” Once again we chose to work with Raman spectroscopy and the compound used was chloroform. At 368 cm-1, the spectrum exhibits the C – Cl umbrella vibration. With a 1 cm-1 resolution the band shows several peaks due to the different relative abundance of both chlorine isotopes in nature. Knowing that 35Cl has an abundance of 75.77 % and 37Cl one of 24.33 %, it is therefore possible to predict the overall probability of each vibration (see Table 3)
| Isotope mass | Required isotope | Probability product | Nº of permutation | Overall probability |
| 118 | 35 35 35 | (0.7577)3 | 1 | 0.4350 |
| 120 | 35 35 37 | (0.7577)2x0.2433 | 3 | 0.4190 |
| 122 | 35 37 37 | 0.7577x(0.2433)2 | 3 | 0.1345 |
| 124 | 37 37 37 | (0.2433)3 | 1 | 0.0144 |
| Sum | 1.00 |
Table 3.
The following figure shows the high resolution spectrum of CHCl3 in the 368 cm-1 region.
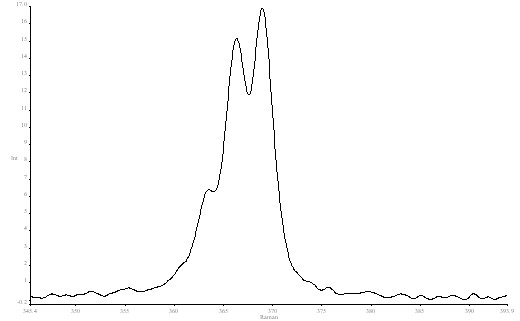
Figure 6. High resolution spectrum of Chloroform in the 368 cm-1 region.
The software used to do the deconvolution was GRAMS/32. The results are presented in the following figure and table.
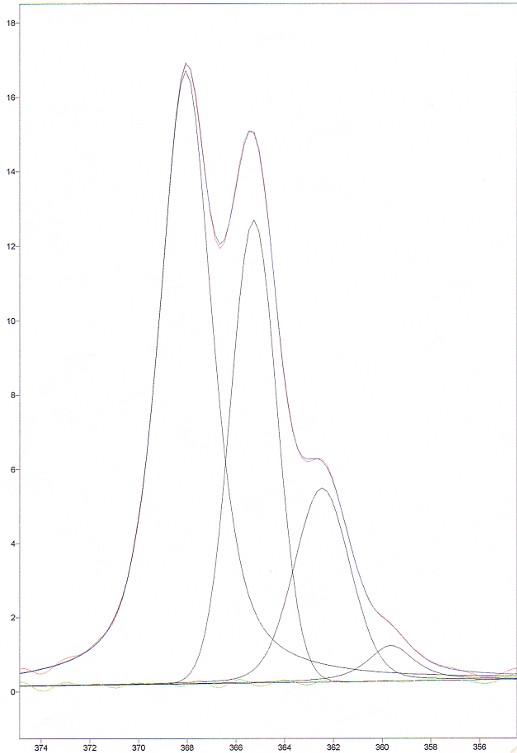
Figure 7. Deconvolved spectrum of CHCl3
| Peak | Isotope | Position | Intensity | FWHM |
| 1 | 35 35 35 | 368.07 | 16.485 | 2.5844 |
| 2 | 35 35 37 | 365.28 | 12.458 | 2.2305 |
| 3 | 35 37 37 | 362.47 | 5.2314 | 2.6893 |
| 4 | 37 37 37 | 359.64 | 0.96015 | 2.2434 |
Table 4.
It is now possible to compare the deconvolution peaks intensity and the theory prediction (see Table 5)
| Peak | Predicted Intensity | Deconvolution Intensity | Deconvolution normalised Intensity |
| 1 | 0.4350 | 16.485 | 0.46 |
| 2 | 0.4190 | 12.458 | 0.36 |
| 3 | 0.1345 | 5.2314 | 0.15 |
| 4 | 0.0144 | 0.96015 | 0.03 |
Table 5.
The first remark is that the intensities of the deconvolved peaks do not match the predicted intensities, especially for peak #2 and #3. One possibility is that the 2 middle modes are asymmetric. This must have an effect on the Raman scattering. However, it is very difficult to evaluate it.
The other remark that can easily been made is that the FWHM of the deconvolved peaks is not constant. We think, however, that in this case, they should be the same. This comes from a limitation of the software used. Hence, this introduces another source of error when calculating the the area of the peaks with the software data..
So, the message is clear – view the quantitative significance of deconvolved overlapping bands with caution.
Now, on the same spectrum, we tried to do a deconvolution using an enormous number of peaks. The result is shown in Figure 8.
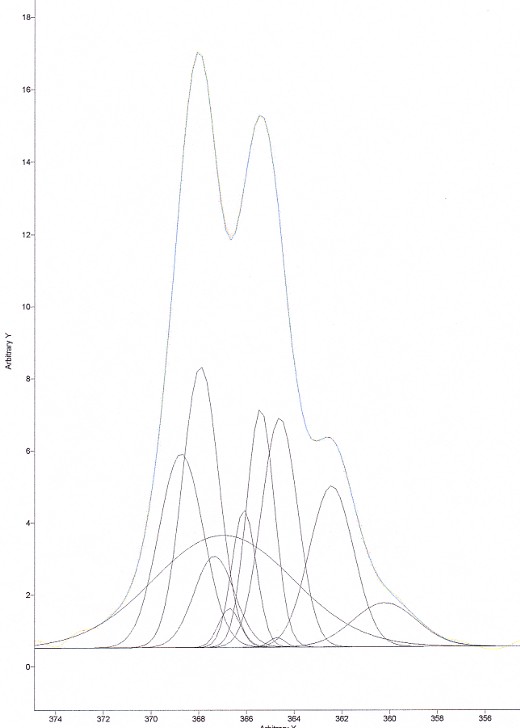
Figure 8. Deconvolution of CHCl3 using far too many bands
As can be seen in Figure 8, the fitting of the curve is PERFECT! However, the result of the deconvolution peaks does not mean anything either…… Put another way, you will be far better off using a restricted number of peaks. A good rule of thumb is: “you should only use the number of peaks that can actually spot in your high resolution spectrum”. So, if you can see 3 peaks, use three peaks to deconvolve your spectrum. You will then limit the error of including peaks that simply don’t exist.
REF: F. Birembaut & P.J. Hendra, Int. J. Vib. Spect., [www.irdg.org/ijvs] 6, 3, 4 (2002)

