Computer-aided Pattern Recognition of Organic Infrared Spectra
Shabsi Walfish, Timothy Sosnowski,
Sara Shraibman, Lok Yung, and John Bové 1
The Cooper Union for the Advancement of Science and Art
Chemistry Department
51 Astor Place,
New York, N.Y. 10003
1author to whom correspondence should be addressed
Abstract
A computer-aided technique has been developed for identification of infrared spectra. This new methodology makes use of simple mathematical techniques to distinguish a targeted spectrum from a group of library spectra. No difficulty is encountered in segregating n-hexane from a number of other tested alkanes. The method proves equally successful when evaluated against other organic functional groups where spectra are similar.
Introduction
An important aid to chemists for the identification of organic compounds is the use of the infrared (I.R.) portion of the electromagnetic spectrum between 4000 cm-1 and 400 cm-1 (2.5 – 25 microns). It is well known that even the simplest of organic compounds is capable of generating a complex I.R. spectrum. These spectra are displayed as plots of percent transmittance vs. wavelength, or as absorbance vs. wavelength. For a successful identification of a sample compound, the reagent in question should be relatively pure, its spectrum adequately resolved and of reasonable intensity. The analyst must also use care that the spectrophotometer is calibrated. Each compound’s spectrum is generally unique, allowing the analyst to compare the unknown reagent to a reference compound.
To help with the identification of IR spectra, different computer aided methods have been developed. These techniques also have the additional advantage of shortening the identification time. In an early study, the investigators used the position of the absorption peaks as their only source for IR identification [2-4]. In two later studies other researchers made use of both peak locations and intensities for spectra identification [5,6]. Artificial neural networks have also been suggested for identification of IR spectra [7,8]. Recently, a coding and retrieval system for IR spectra data has been introduced based on effective peaks matching [9]. The object of this proposed method is to first provide a coding method for IR spectra data, then to develop an objective way of finding effective peaks, and finally to introduce a retrieval system. A number of commercial algorithms are also available for IR spectrum identification. One such example of the commercial use of pattern matching are the algorithms provided by the Galactic Industries Corp. [10]. These matching techniques include a first derivative correlation algorithm and a Euclidean distance algorithm. More recent examples of the application of pattern matching techniques can be found in [11-16].
In an earlier report one of us [1] reported on the application of pattern recognition to the infrared analysis of water samples. We should now like to report a novel technique that makes use of computer aided pattern recognition for analyzing the infrared spectra of organic compounds. Spectra are generated using a Perkin-Elmer FT-IR 1600 Spectrophotometer possessing a resolution of 2 cm-1. The sample compartment of the instrument is fitted with a Spectra-Tech Q-Circle cell [17], an attenuated total reflectance (ATR) based system. It uses an automated pump that draws the sample into the cell, and which is later used to empty the sample cell. The cell is also fitted with a temperature control. For this report the cell temperature was maintained at 27o C. Whenever the cell is emptied, it is washed and flushed several times with an appropriate low boiling solvent (usually acetone), and then dried. The technique has also been used successfully with a SensIR diamond based ATR cell [18].
It is well known in the field of infrared spectroscopy that alkane spectra possess just four major peaks: a C-H stretch at 3000 cm-1, a CH2 bending absorption at approximately 1465 cm-1, a CH3 bending absorption at approximately 1375 cm-1, and a CH2 bending (rocking) motion at approximately 720 cm-1. Because of the similarity of the alkane spectra, it is difficult to distinguish between alkanes without some supporting data such as boiling points or melting points. It is for this reason that we selected the challenging example of several alkanes, along with a number of other organic functional groups, as a test of our computer-aided pattern recognition method.
Experimental
An infrared (IR) spectrum was generated using a FT-IR spectrophotometer (represented by a plot of absorbance vs. wavelength in cm-1). An absorbance data array, A(v), was then produced by subtracting the average value from the original absorbance spectrum (cf. eq. 1).
A(v) = Absorbance(v) – Absorbanceavg (1)
The resulting absorbance spectrum (shifted along the vertical axis) was then normalized to a maximum absolute value of 1.5 (cf. eq. 2).
A'(v) = 1.5 A(v) / |A|max (2)
This normalized array of absorbance vs. wavelength data points were then used to generate a new function, representing the integral of the normalized absorbance (cf. eq. 3).
I(ν) = ʃ A’ (ν’) dν’ 700≤ ν ≤ 4000 (3)
While we chose to use an integration range of 700 – 4000 cm-1 for purposes of this report, the experimenter is free to select any other convenient range he may find useful. In fact the results can be improved dramatically by focusing the integration range on an appropriate region of the spectrum (e.g. for alkanes narrowing the range to 2800 – 3200 cm-1 results in considerably increased accuracy). A new data array I‘(v) was then obtained from I(v) by multiplying by a factor of 100 and dividing through by the maximum magnitude of I(v) (cf. eq. 4).
I’ (v) = 100 I(v) / |I|max (4)
Finally, the values that result in the array were used as a reference to compare with other I‘ arrays (generated in a similar manner). This comparison was then used to determine whether a statistical match was produced. For purposes of experimental preference, one can define a reference sample as the result of one generated spectrum or the average of several spectra. The reference I‘ array may be labeled I‘R(v) and the test spectrum can be labeled I‘S(v). For purposes of comparison a rho array may then be derived as follows:
rho(v) = I‘S(v) – I‘R(v) (5)
A plot of rho(v) represents a “difference spectrum”, indicating the nature of the differences between the sample spectrum and the reference spectrum. The maximum magnitude of the absolute value of this difference spectrum, |rho(v)|max, is the minimum fitting tolerance, Rho, for which the sample spectrum matches the reference spectrum. Additionally, one can plot the variation between the two data sets relative to a selected maximum fitting tolerance (as when testing for a match / no match case against a reference spectrum). An R(v) array may be produced which represents the deviation from the reference spectrum as a fraction of the selected maximum tolerance (in other words, a normalized version of the rho(v) array). This is summarized in equation 6.
R(v) = ( I‘S(v) – I‘R(v)) / rho (6)
The resulting R(v) array may then be plotted against two horizontal lines that are assigned values of -1 and 1 respectively. If all the values within the array lie between -1 and 1, the sample is accepted as a match to the reference spectrum. A non-match is shown as an R(v) plot in which part of the graph exceeds the constraints of the lines at –1 and 1, representing a deviation greater than the selected fitting tolerance rho. This analysis is summarized in Figures 1 and 2.
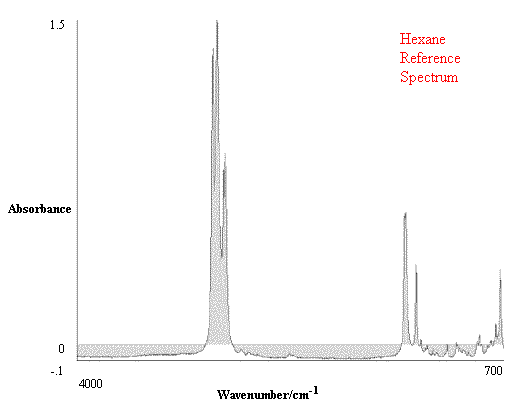
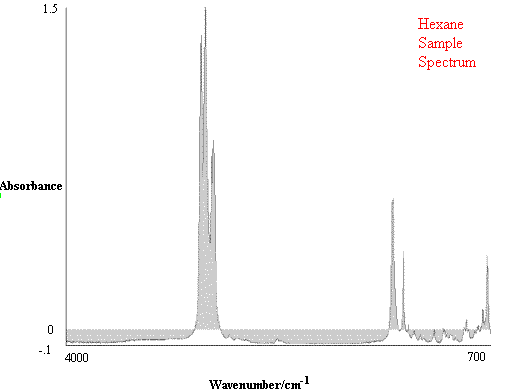
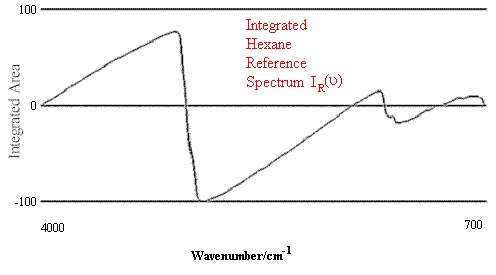
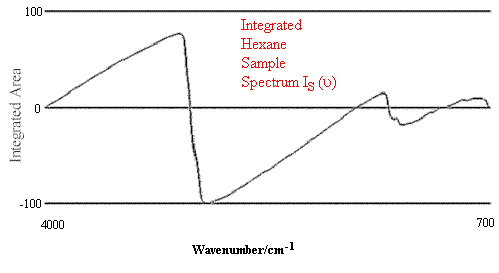
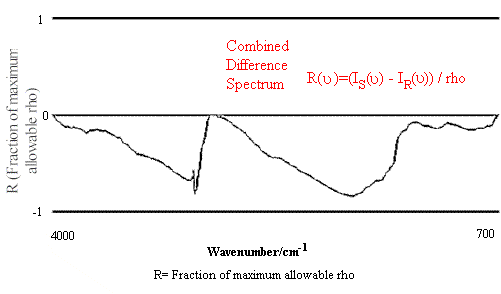
Figure 1. Comparison of Hexane Reference vs. targeted Hexane Sample.
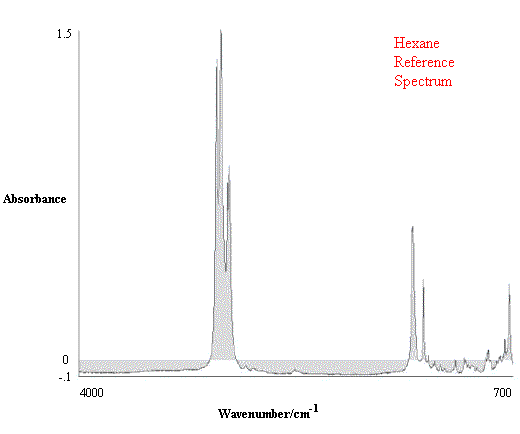
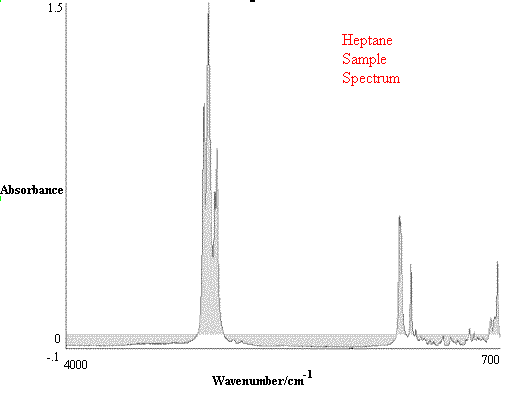
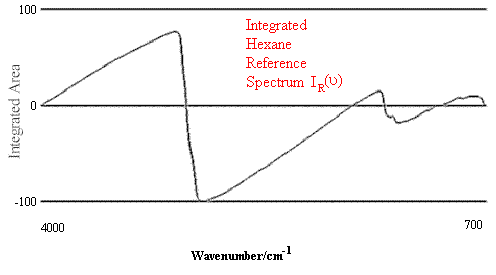
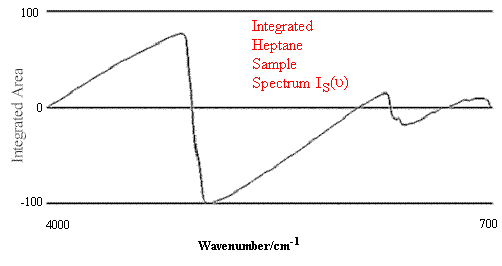
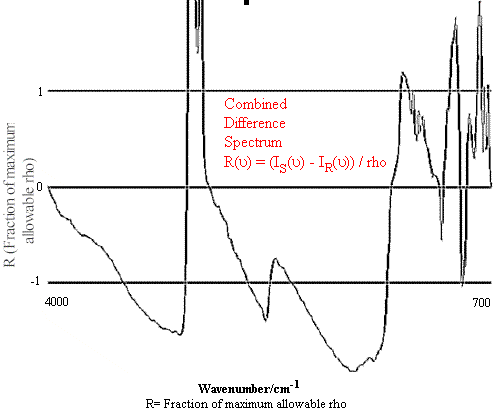
Figure 2.Comparison of Hexane Reference vs. targeted Heptane Sample.
Figure 1 contains the spectrum match of a hexane sample vs. a hexane reference. One can see that in this case the rho tolerance has not been exceeded, and that the values remain within the two parallel lines. In the second case, illustrated in Figure 2, where there should be no match between hexane and heptane, the rho tolerance between the two parallel lines has been exceeded in several places. In addition, this technique reveals where the violations occurred in the architecture of the I.R. spectrum, and that (in the case cited) the location of the major difference was in the 3000 to 2800 cm-1 region of the spectrum.
Thus, the largest value produced by equation 4 defines the maximum difference of any two points with the same wavenumber in the integral of the absorbance spectrum (normalized to 100). This fitting tolerance, Rho, may then be compared to the fitting tolerances obtained by comparison with other reference spectra in order to determine a best fit. A smaller value of Rho indicates a better match. It should be noted that at the edges of the spectrum, the Rho sensitivity will be at a minimum. This is because the shape of the integral must converge to zero at these points.
Results
Preliminary results indicate that this computer-aided method successfully selected and identified all of the tested compounds. Since the alkane series was selected as a challenging case, hexane was picked as a critical referee example. The hexane reference IR spectrum was compared to several alkanes and to spectra belonging to a number of other functional groups. The computer-aided technique had no difficulty selecting the corresponding library spectrum for each of the reagents tested. For example, when the normalized average Rho value of hexane was compared to that of heptane, octane, nonane, and decane, Rho values of 2.56, 4.18, 4.83, and 6.13 respectively resulted. Other Rho values for several other common functional groups are summarized along with the alkanes in Table 1. and in Figure 3. Step discontinuities in the results for hexane and heptane are visible because some of the samples were taken several months after the original data were collected, during which the instrument was serviced. After the instrument was serviced, the quality of the discrimination was noticeably improved. In spite of this drastic source of experimental error (the spectra were visibly distorted prior to the servicing), the technique was still able to correctly identify the reagents in question. All of the groups tested far exceeded the Rho values of the alkanes, providing additional evidence for the discriminating quality of the method.
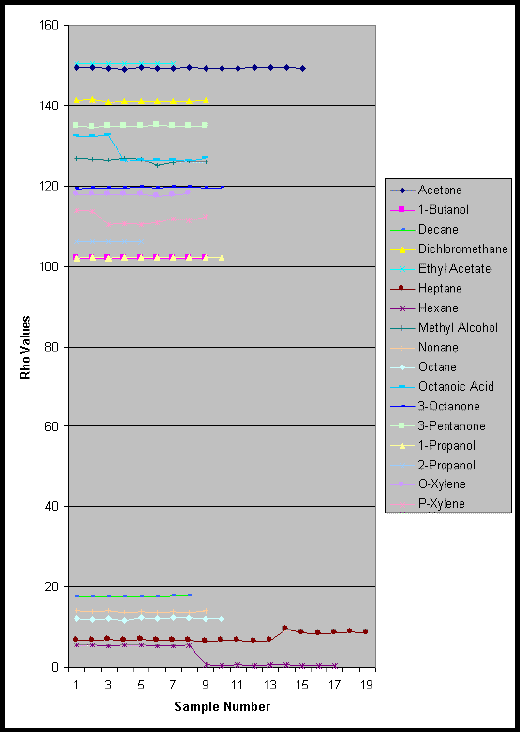
Figure 3. Summary of Rho Values vs. Sample Number using a hexane reference.
|
Compounda |
Trials |
Rho (average) |
Rho (S.D.) |
Rho Normalized To Hexane Rho |
| Acetone |
15 |
149.4 |
0.091 |
51.50 |
| 1-Butanolb |
9 |
102.0 |
0.040 |
35.16 |
| Decane |
8 |
17.80 |
0.144 |
6.133 |
| Dichloromethaneb |
9 |
141.2 |
0.186 |
48.68 |
| Ethyl Acetateb |
7 |
150.5 |
0.034 |
51.88 |
| Heptane |
19 |
7.416 |
0.985 |
2.556 |
| Hexane |
17 |
2.901 |
2.525 |
1 |
| Methyl Alcohol |
9 |
126.3 |
0.601 |
43.54 |
| Nonane |
9 |
14.01 |
0.216 |
4.829 |
| Octane |
10 |
12.14 |
0.194 |
4.183 |
| Octanoic Acidb |
9 |
128.4 |
2.966 |
44.27 |
| 3-Octanoneb |
10 |
119.5 |
0.134 |
41.20 |
| 3-Pentanoneb |
9 |
134.8 |
0.163 |
46.48 |
| 1-Propanol |
10 |
102.2 |
0.062 |
35.23 |
| 2-Propanol |
5 |
106.3 |
0.048 |
36.63 |
| P-Xyleneb |
9 |
111.7 |
1.317 |
38.50 |
| O-Xyleneb |
8 |
117.8 |
0.185 |
40.60 |
Table 1. Summary of FT-IR Results
a All compounds purchased from Aldrich Chemical Co. HPLC grade unless otherwise noted.
b Compound is 99% purity.
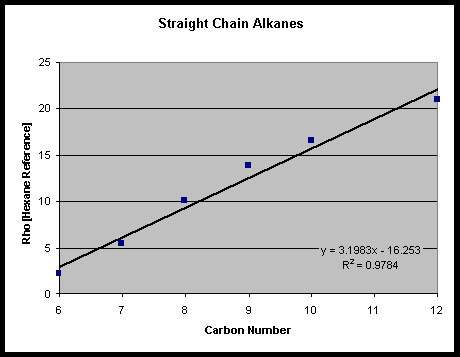
Figure 4. Linear fit for Rho c vs. Alkane Carbon Numbers 6 to 12 c Rho values for this chart were produced from IR spectra obtained using a SensIR diamond based ATR cell.
Conclusion
This new computer-aided method for identifying IR organic spectra shows important potential for identifying IR spectra. Unlike many other pattern recognition techniques, this technique provides a visual means of identifying the nature of the discrepancies between two IR spectra. Furthermore, the linear trend in the alkane fitting tolerances demonstrates that the rho values produced by this technique are related to the reagent itself, and are not merely arbitrary values. The technique is also computationally simple (in fact, the integrated spectra can even be pre-computed and stored for faster searching). Thus, it should be suited for building a more comprehensive library of referee compounds. It should also be possible, with further effort, to extend the use of this technique to the area of quality control. Work is also underway to extend a modified version of this methodology to include the identification of Raman spectra. This procedure should give one the ability to study water-soluble compounds.
References
- Witelski, T.; Ng, P.; Ying, J.; Lundy, J.; Bové, J. Intern. J. Environ. Anal. Chem, 1990, 44, 127-136.
- Anderson, D.H.; Covert, G.L. Anal. Chem., 1967, 39, 1288.
- Erley, D.S. Anal. Chem., 1968, 40, 894.
- Rann, C.S. Anal. Chem., 1972, 44, 1669.
- Fox, R.C. Anal. Chem., 1976, 48, 717.
- Tanabe, K.; Tamuea, J.; Saeki, S. Anal. Chim. Acta., 1979, 112, 211.
- Ying, L.S.; Levine, S.P.; Tomelline, S.A.; Lowry, S.R. Anal. Chem., 1987, 59, 2197.
- Luinge, H.J.; Leussink, E.D.; Vissek, T. Anal. Chim. Acta., 1997, 345, 173.
- Lau, O.W.; Hon, P.K.;Bai, T. Vibrational Spectroscopy, 2000, 23, 23-30.
- Galactic Industries Corp.395 Main Street, Salem, N.H. 03079 USA
- Schurmann, J. Pattern Classification, a unified view of statistical and neural approaches; John Wiley & Sons: New York, 1996.
- Ripley, B. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, 1996.
- Bishop, C.M. Neural Networks for Pattern Recognition; Clarendon Press: Oxford, 1995.
- Wood, J. Pattern Recognition, 1996, 29 no. 1, 1-17.
- Smetanin, Yu. G. Pattern Recognition and Image Analysis, 1995, 5 no. 2, 254-293.
- Solomons, T.W. Organic Chemistry, 6th Ed.; John Wiley & Sons: New York, 1996; p 141.
- Spectra-Tech Inc., 2 Research Drive, P.O. Box 869, Shelton, CT 06484 USA.
- SensIR Technologies, 15 Great Pasture Road, Danbury, CT 06810 USA
Received 13th January 2001,received in revised format 21st February,
accepted 21st February 2001.
REF: S. Walfish, T. Sosnowski, S. Shraibman, L.Yung, and J. Bové. Int. J. Vib. Spect., [www.irdg.org/ijvs] 5, 2, 5 (2001)

