Applications of Raman Microspectroscopy in the Field of Semiconductors
6. Applications of Raman microspectroscopy
in the field of semiconductors
T. Jawhari (a) and A. Pérez-Rodríguez (b)
(a) Serveis Científico-Tècnics,
Universitat de Barcelona,
08028, Barcelona,
Spain
e-mail: jawhari [at] giga.sct.ub.es
(b) Dept. d’Electrònica,
Universitat de Barcelona,
08028 Barcelona,
Spain
e-mail: perez-ro [at] el.ub.es
Introduction
We all know the importance of microelectronics in our everyday life and the huge advances that occur continuously in small geometry devices and integrated circuits. This is, for example, well reflected by the astonishing fast changes that take place incessantly in the field of computers. The rapid evolution in semiconductor technology, including device fabrication, thin-film deposition, interface preparation and microelectronic processing, have increased the need for characterization techniques that can provide more precise information, especially on the structure of the materials. The quality of this information is one of the most critical factors in designing and manufacturing microelectronic devices since high performance integrated circuits and devices demand an excellent quality material, either in the form of bulk material, thin-film or device structure. Furthermore, in the last few years there has been a new interest in silicon (Si) technology, related to the development of Micro-Electro-Mechanical Systems (MEMS) in which sensor devices and micro-actuators are integrated together with the electronic circuits for signal processing and control. In such systems, the characterization of the electrical, optical, mechanical and thermal properties of the thin films and structures are also critical for the performance of the device. The study of both crystallographic and physical features of the structure is of high technological interest in order to improve the process steps in MEMS technologies.
Raman scattering is an extremely powerful contactless tool which allows non destructive and quantitative microanalysis of structural and electrical properties. This technique is very useful since the Raman signal is very sensitive to the microstructural state of the sample and other local environments giving therefore information on the structure of the material on the scale of a few lattice constants. Raman signal is a function of the electron-phonon interaction, i.e. lattice vibration, and is a good complementary method to other techniques used in the characterization of the solid state such as transmission electron microscopy (TEM), X-rays diffraction, X-ray photoelectron spectroscopy (XPS), secondary ion mass spectroscopy (SIMS), Auger electron spectroscopy, etc. Most of these techniques require a sample preparation that often alters the material whereas, in principle, the Raman technique does not affect the sample at all which is a crucial point when characterizing processed devices. Another major advantage of Raman spectroscopy is that when combined to a microscope, the technique can probe smaller dimensional scale devices. This is important for the analysis of microstructures and devices, where the properties of the layers are strongly process dependent and may differ significantly from the bulk material properties. Therefore, the micro-Raman system is now one of the preferred methods when characterizing semiconducting materials.
We shall here illustrate the possibilities that offer micro-Raman spectroscopy in semiconducting materials with examples obtained in the Raman laboratory of the Serveis Científico-Tècnics in collaboration with the Department of Electronics of the University of Barcelona. These studies are mainly centred in the analysis of structures and processes in Si and group IV technologies (SiGe and Si based alloys, SiC…). In principle, Si constitutes the main material for electronic devices and integrated circuits. In this sense, the maturity reached in Si technology has allowed the development of high performance devices, which may include heterostructures with SiGex and, more recently, more complex SiGexCy and SiCy based alloys. This deep knowledge in the Si based technology has also been applied for a wide range of sensor and MEMS devices, constituting the basis of the Si micromachining technologies. Other group IV semiconductor, which now constitutes an emerging technology, is SiC due to its potential applications for high temperature, high power electronics and sensors working in harsh environments. This is related to the electronic and mechanical properties of this compound, such as wide energy band gap (2.4 to 3.2 eV, depending on the polytype), high thermal conductivity, mechanical strength, high breakdown electrical field (i.e., ability of the material to stand high electrical fields), and extreme chemical inertness even at high temperatures. The examples presented here are representative of the wide range of characterisation problems related to semiconductor based materials and structures which can be solved by the micro-Raman probe.
Instrumentation
The great advances made in Raman microscopy since its discovery in the mid-seventies were fundamental in the applications of Raman spectroscopy to semiconductor devices since it provides a structural and molecular picture with a very high spatial resolution. The schematic diagram of the Raman instrument Jobin Yvon T64000 used at the University of Barcelona is shown in Figure 1. This spectrometer can work either in the micro-mode utilizing an optical microscope or in macro-mode with a conventional macro-chamber. For semiconducting materials, excitation source is usually provided by a typical Argon ion laser which emits discrete lines between 458 and 529 nm, with its two main lines at 488 nm and 514.5 nm. Sometimes other lines than the two main ones are used when analysis at different depth penetration is required. For these materials, changing the laser line from the green (514 nm) to the dark blue-violet at 458 nm will diminish the penetration depth. In the case of crystalline silicon, the penetration depth of the light in the back-scattering configuration has been estimated to be approximately 300, 600 and 800 nm for laser excitation at 458, 488 and 514 nm, respectively[1]. Higher penetration depth can be achieved by decreasing the excitation energy, as optical absorption decreases for energies in the visible-near infrared (NIR) region. For this, a titanium-sapphire laser can be coupled to the argon ion laser. This provides radiation in the NIR in a continuous way between 700 and 900 nm. The use of a NIR laser can sometimes be worthwhile, especially for Raman resonance measurements since many semiconductors have their electronic gap in the near infrared.
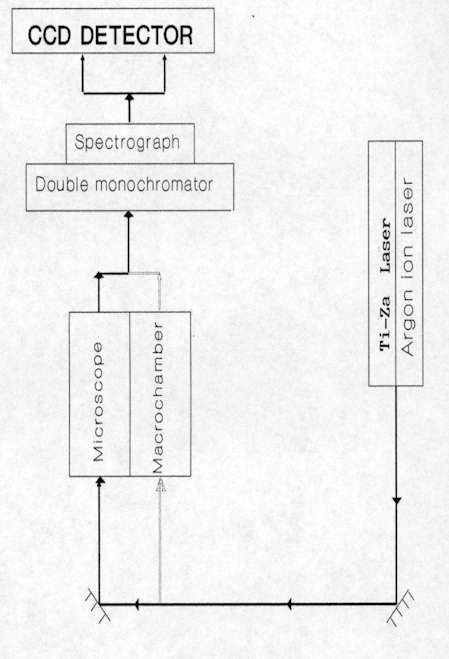
Figure 1. Schematic diagram of the Raman spectrometer
This instrument comprises of a double monochromator and a spectrograph that disperses the Raman scattered light onto a CCD detector cooled with liquid nitrogen.
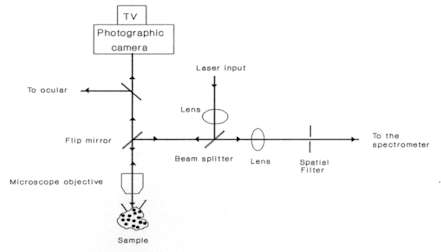
Figure 2. Entrance optics of the micro-sampling system
As can be seen in Figure 2, the incident laser beam is reflected by a beam splitter and a flip mirror onto the microscope objective. This focuses light onto the sample. The scattered light is recollected by the same microscope objective (back-scattering configuration), passes through the beam splitter and is focused onto the entrance slit of the spectrometer. The flip mirror situated in the microscope also permits us to visualize the microscopic region under analysis with the TV camera. In the case of materials opaque to the laser, such as most semiconductors, the visualization of the sample in the camera must be achieved with a bright field reflection illumination system. The advantage of using a back-scattering set-up, as shown in Figure 2, is that the laser spot on the sample can be directly observed on the TV monitor which allows precise identification of the microscopic region of the sample analyzed.
When maximum lateral and axial resolution is required, a spatial filter, which consists of a pinhole, is placed behind the microscope at the image plane. This rejects scattered light originating from outside of the laser focal volume.
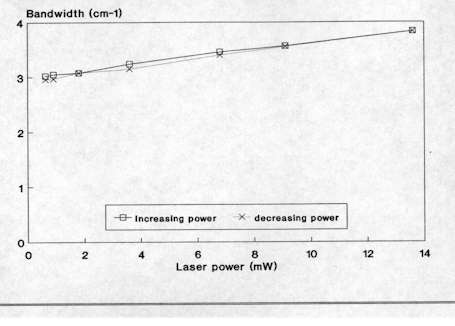
Figure 3. Effect of laser power on the Raman spectrum of Si
(bandwidth vs power)
As already mentioned, micro-Raman spectroscopy allows analyses of many kinds of materials with no sample preparation. Solids are easily studied by placing them on a standard glass microscope slide. However, with a Raman instrument coupled to an optical microscope, it is sometimes necessary to take some precautions due to the high power density, typically between 104-105 W cm-2, as a result of tight focusing of the laser beam that is obtained with the microprobe. This may cause those samples with high optical absorption in the spectral region close to the laser frequency to be physically affected by local heating. Sometimes, a small black patch of the size of the focused laser spot appears due to local annealing. This local heating can also affect the shape and position of the Raman bands. For example, in Figure 3 we can see that the bandwidth of the Si Raman band at 520 cm-1 increases as the laser power augments. This phenomenon is not due to local degradation of the crystal, but only related to the local heating of the crystalline network which causes anharmonic effects in the spectra. Accordingly, this effect is totally reversible and is determined by the temperature gradient achieved in the scattering volume. For highly damaged or amorphous semiconductors, absorption of light increases and more intense thermal effects are observed. Other laser power effects such as wavenumber shift were sometimes observed. This is illustrated in Figure 4 which shows how the low frequency mode of CuS increases as the laser power is increased from 1.2 mW to 5.0 mW. This shift effect was also observed to be entirely reversible. These series of measurements were carried out in Cu-rich CuInS2 layers of a solar cell device, where CuS was found to appear as a secondary phase. All these results clearly imply the need to carefully test the possible presence of thermal effects in the spectra when using a micro-Raman probe. Typically, for a X100 microscope objective, the laser power at sample should be preferentially between 1 and 2 mW whereas with a X50 objective the laser power can be as high as 5 mW.
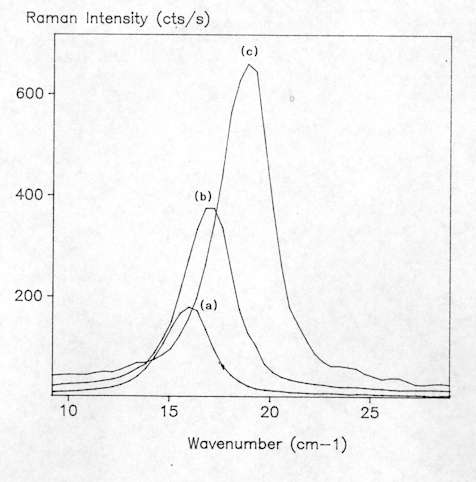
Figure 4. Raman spectra of CuS recorded at different laser points:
(a) 1.2mW, (b) 2.5mW, (c) 5.0mW.
Spatial resolution
An important point that has to be considered in microanalysis is the spatial resolution. Two different spatial resolutions can be separated in Raman microspectroscopy; namely, lateral and axial resolutions. Most of the manufacturers of micro-Raman instruments give a value for the lateral spatial resolution of 1 m m or even less which in fact corresponds to the theoretical diffraction-limited spot (1.22 /N.A.). For instance, a typical x100 microscope objective used in the Raman microprobe experiment with a N.A. of 0.95 and
=488 nm would produce a theoretical spot diameter of 0.62 µ m. Therefore, submicron lateral resolution is achieved and thus allows the characterization of some specific and localized regions in single devices in an integrated circuit.
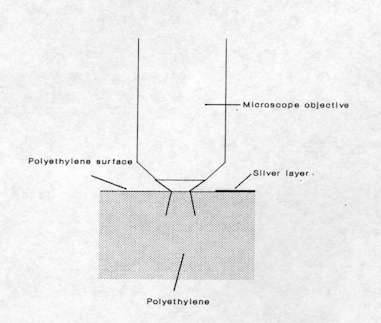
Figure 5. Experimental configuration for the determination of lateral resolution in a PE-silver layer system
The lateral spatial resolution has been checked in the conditions of routine micro-Raman experiment by recording successive Raman spectra at different positions across a polyethylene (PE)-silver layer interface. The experiment was achieved by preparing a neat interface through vacuum-deposition of an extremely thin silver layer on a flat polyethylene surface and using a microscope xy translation stage controlled by a computer to probe the Raman signal across the interface (see Figure. 5). The intensity of the Raman band of polyethylene at 2884 cm-1 was measured for each spectrum recorded and plotted in function of the analyzed position as shown in Figure 6. The experiment was first carried out without any diaphragm and then repeated with a
400 µ m diameter pinhole situated at the back image plane of the microscope (i.e. the confocal arrangement), the microscope objective being a X100/0.95 N.A. From these data, it can be deduced that the lateral resolution for routine micro-Raman work is of the order of 2 µ m but can be improved to 1 µ m when using a 400 µ m pinhole in the confocal plane[2].
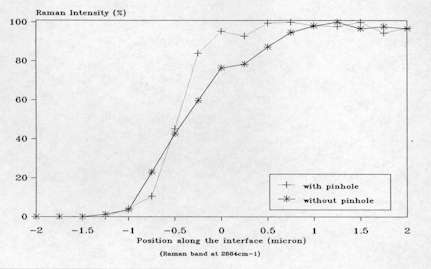
Figure 6. Raman intensity of PE vs position across the PE-silver interface.
As already indicated, most semiconductors have a high optical absorption in the spectral range of the laser frequency. In this case, the axial resolution of the micro-Raman spectrometer is higher than the penetration depth of light, therefore the depth of the scattering volume is determined by the optical absorption. However, this is not the case for wide energy band gap semiconductors such as SiC or GaN. These semiconductors have a low optical absorption in the visible region, and are now receiving special interest in the field of high temperature applications and optoelectronic devices in the blue part of the spectrum. For these semiconductors, the minimum depth of the scattering volume of collected photons can be estimated from the theoretical nominal depth of field of the microscope objective, given by /N.A.2, where
is the excitation wavelength and N.A. the numerical aperture of the objective. In reality, the axial resolution is of few microns and will depend very much on the diameter of the pinhole used in the confocal plane.
Applications
First of all, we shall examine the different parameters that can be obtained from the Raman spectrum of solid state materials and analyze the type of information on their structure and physical properties they can offer.
a) Frequency
The frequency of the phonon Raman band depends on the interatomic forces (i.e. force constants of the bonds), the bond length, the masses and positions of the atoms and any effect affecting these features will produce a change in the frequency of the band. Hence, the band is sensitive to the presence of stresses or strains in the scattering volume: a tensile stress will determine an increase in the lattice spacing and, hence, a decrease in the wavenumber of the vibrational mode. In the case of compressive strain, the decrease of the lattice parameter yields a corresponding increase of the vibrational frequency. In the elastic regime, these shifts depend in a linear way on the magnitude of the stress, and the position of the Raman band can be used to measure the stress.
On the other hand, the presence of crystalline disorder also gives rise to changes in the frequency of the band, usually towards lower wavenumbers. These are related to the breaking of translational symmetry in the crystal, which can be produced by structural defects such as dislocations or by grain boundaries in nanocrystalline materials. The position and shape of the Raman band can be simulated with a correlation length model[3] which allows to estimate the value of the correlation length L from the analysis of the Raman band. This correlation length is defined as the characteristic size of crystalline domains in the scattering volume where the translational symmetry of the crystal holds, and is related to the average distance between defects for damaged crystals or to the grain size for nanocrystalline materials.
Other parameters affecting the frequency of the Raman band are the temperature which affects the contribution of anharmonic effects and the presence of chemical impurities in the crystalline network which leads to changes in the mass of the atoms in the lattice sites. For example, the presence of Ge atoms at substitutional positions in the Si network produces a decrease in the frequency of the vibrational modes, due to a higher mass. This is known as the chemical effect. Besides, the presence of impurities at substitutional positions also affects the lattice spacing due to the different size of the impurity. Hence, a stress effect will also occurs in addition of the chemical one.
b) Raman bandwidth
Raman bandwidth and bandshape are closely related to the crystalline order. In principle the bandwidth is related to the lifetime of the phonons. The presence of crystalline disorder produces a decrease of the phonon lifetime which thus generates an increase of the bandwidth. Therefore the density of defects can be evaluated from the bandwidth. On the other hand, the bandshape of the Raman line is also affected by confinement of phonons (for example in the case of polycrystalline structures where the phonons are confined in crystalline grains of average size L), being that given by the correlation length model. The fitting of both the bandshape and the frequency position of the Raman line with this model allows us to estimate both correlation length and average stress in the scattering volume. This is interesting for nanocrystalline materials where average grain size is given by the correlation length. The main limit for this measurement is that phonon confinement only occurs for sizes in the nanometric range (L<20nm for Si).
Nevertheless, we have also to bear in mind that all the features affecting the frequency of the Raman band can also give rise to a band broadening if gradients are present in the scattering volume, such as temperature gradients produced by the gaussian like profile of the incident beam in the light spot, or strain gradients in the layers.
c) Raman intensity
The intensity of the Raman band is also very sensitive to the structure of crystals and as a result significant information can be obtained from intensity measurements. Damage in the lattice leads to a decrease of the intensity of the first order modes, related to the breaking of bonds and changes in atomic forces displacements, and, hence produces a decrease of the Raman polarizability tensors. For example, ion bombardment during doping process will alter the original crystal with a consequent reduction of the Raman signal intensity. Intensity measurement is also performed for quantitative analysis of different polymorphisms, defects, disorder, micro-inhomogeneities, etc.
The strong dependence of the Raman experimental data (frequency, bandwidth and Intensity) on the structural features in the scattering volume calls for the extremely accurate measurement of the Raman line. For this, the experimental conditions should be as stable as possible. One of the main factors that affects the stability of the peak position is the temperature in the room where the spectrometer is installed. Variation in the lab temperature produces subtle mechanical changes in the diffraction gratings and optical parts. When high resolution measurements are required, the lab temperature stability should be better than ± 1oC. Moreover, the intensity of the Raman line can also be affected by possible dispersion of light by dust particles in the air, as well as on the measuring surface and mirrors. Some of these effects can be corrected (mainly the frequency shift) by measuring reference samples with well known bands, such as a single crystal reference Si wafer (520 cm-1). Another possibility is to use the plasma lines of the laser beam as internal calibration lines.
Examples of applications
The first order Raman spectrum of crystalline Si has a well defined single line at about 520 cm-1. This line has a Lorentzian shape, with a full width at half maximum of approximately 3 cm-1. As already indicated, this line is extremely sensitive to the presence of stress. In a biaxial stress (i.e. stress components in the plane of the sample surface) in elastic regime, the stress can be obtained from:
= 250 .
Mpa/cm-1
where is the frequency shift in wavenumber. Since the fabrication processes of semiconductors devices often produce strains in some localized region, the micro-Raman probe was found very useful in analyzing these small domains. For instance, this technique is now recognized as a powerful tool in identifying stress and strain in polycrystalline silicon structures used for the fabrication of large polysilicon micromechanical structures[4-6]. These micromechanical systems based on surface-micromachining technologies can have serious stress effects that can cause mechanical device failure, curling or fracture. Figure 7 shows the stress depth profile of a phosphorus implanted LPCVD (Low Pressure Chemical Vapour Deposition) polysilicon layer. The stress values obtained from the micro-Raman analysis were in good agreement with those based on mechanical deformation measurements[5].
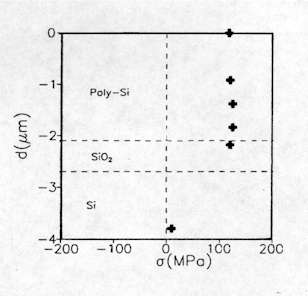
Figure 7. Stress (s) depth profile in a phosphorous implanted LPCVD polysilicon layer where d is the distance from the top surface.
On the other hand, the measurement of the intensity of the Raman band has been applied to quantify the residual damage in processed wafers, such as ion implanted ones. Figure 8 shows an example on the quantification of the implanted induced damage in wafers of 6H-SiC (an hexagonal polytype of SiC) implanted with different doses of Ge+ ions[7]. This is performed by the normalised intensity In=(Io-I)/Io, where I is the intensity of the Raman band measured in the implanted layer and Io is the intensity of the Raman band measured in a virgin non processed sample. For a low degree of damage, I is very similar to Io and In is close to 0. As damage increases, I decreases and In tends to the maximum value of 1. This gives a 100% of damage which corresponds to the damage level for which fully amorphization of the implanted layer occurs. In this case, all the crystalline modes vanish from the spectrum, and I becomes 0. Figure 8, which gives the intensity variation of the Longitudinal Optical (LO) peak of SiC at 967 cm-1, indicates how the crystalline structure is progressively destroyed as the implanted dose of Ge+ is increased. This method allows the degradation of the crystalline structure to be followed. It is also used to optimize the annealing process after ion implantation in order to eliminate the induced damage.
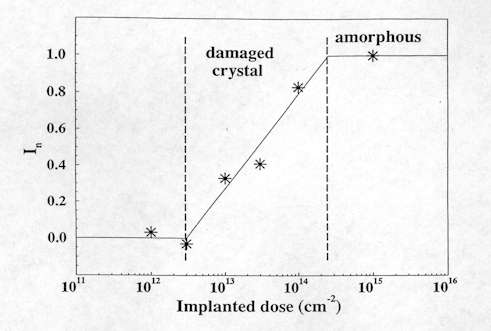
Figure 8. Relative intensity variation of the LO 6H-SiC peak in relation to that of the reference material versus the inplantation dose
Furthermore, the changes in the bandshape and position of the Raman band related to phonon confinement allow the assessment of the average grain size and stress in nanocrystalline Si layers[8], as well as the density of defects in highly damaged Si films[9]. Figure 9 shows the spectra simulated for Si assuming spherical confinement and different values of the correlation length L. As can be seen, for values of L below 20 nm the Raman band is shifted towards lower frequencies and asymmetrically broadened, and both band shift and broadening increase as L decreases. However, in general the application of these models for grain size assessment has to take into account the fact that these are very simple models in which stress is assumed not to affect the shape of the Raman line and both stress and correlation length are assumed as uniform in the scattering volume.
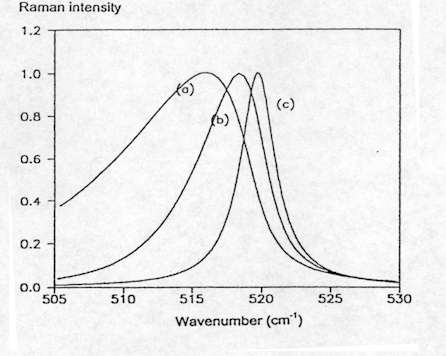
Figure 9. First order Si Raman spectrum simulated assuming spherical confinement: (a) L = 60° Å, (b) L = 100° Å, (c) L = 200° Å
Raman spectroscopy can also be used as an interesting alternative method to X-ray diffraction for the characterization of heteroepitaxial layers. The Raman spectrum of SiGex alloys presents three main lines, related to Si-Si at about 500 cm-1, Si-Ge around 400 cm-1 and Ge-Ge about 300 cm-1 vibrational modes (see Figure.10). It was shown[10] that the wavenumber of these modes present a linear relationship with both chemical composition and strain:
Si-Si = 520 – 68x – 830
Si-Ge = 500.5 + 14.2x – 575
Ge-Ge = 282.5 + 16x – 384
where is the wavenumber of the Raman mode, x the chemical composition and
the strain parallel to the substrate. Using these relationships, a single Raman spectrum of SiGex allows the determination of silicon and germanium contents as well as strain. Similar relationships have also been proposed for SiCy as well as for more complex SiGexCy and SiGexBy ternary alloys[1,11].
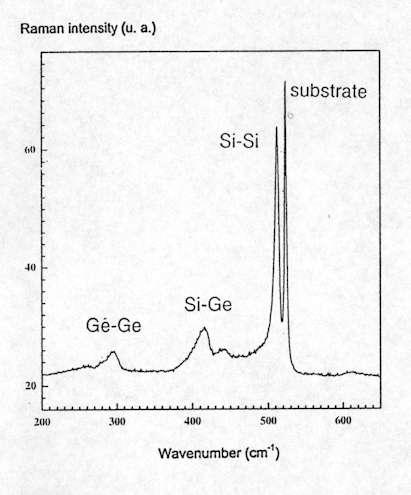
Figure 10. Raman spectra of SiGe0.3, showing the Si-Si, Ge-Ge and Si-Ge vibrational modes.
The Raman band at 520cm-1 is due to the crystalline Si substrate.
The high spatial resolution achieved with the Raman microprobe enables in depth study of complex multi-layered structures, such as Silicon-On-Insulator (SOI)[12-14]. SOI wafers are used for the fabrication of sub-micron Complementary Metal-Oxide-Semiconductor (CMOS) devices and integrated circuits for high frequency and/or high radiation level applications (such as for space electronics). A typical method used to carry out depth profiling in the multi-layer structure is to record measurements performed at different positions along the surface of the sample that has been previously bevelled at a low angle (Figure 11). Figure 12 shows the Si spectra measured at different positions from the SOI structure schematically represented in Figure 11. For this structure (which is not representative of the high quality state of the art material), structural degradation was observed in the region close to the Si/SiO2 interface, which is clearly observed from the changes of the Raman line. More recently, this method has also been successfully applied for the analysis of InAlAs/InGaAs/InP structures for high electron mobility transistor devices[15].
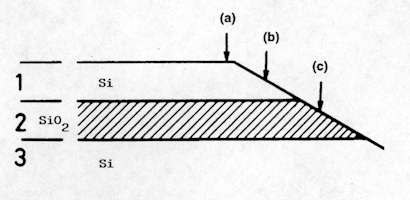
Figure 11. Diagram showing several points along the bevelled Si-SiO2-Si structure where the micro-Raman spectra were recorded.
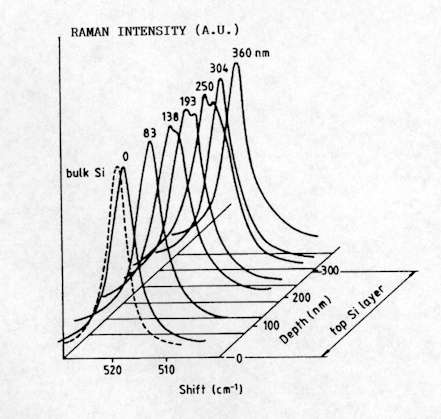
Figure 12. Micro-Raman spectra recorded along the bevelled structure, where d is the distance from the top Si surface.
Mapping measurements can also be performed, providing a non destructive and simple way for the analysis of the thickness and structural uniformity of thin films, such as cobalt silicide films (CoSi2) deposited on Si for IR detectors[16] This was performed by measuring the intensity of the Raman signal from the Si substrate at different points on the surface. As can be seen in Figure 13, the intensity of the Raman line of the substrate decreases in an exponential way as the thickness of the layer increases. This is due to absorption of light in the layer. This method allows detection of CoSi2 films as thin as 3-4 nm, and the CoSi2 film thickness can be measured in the range between 10 and 100 nm with an uncertainty below 10%, provided that optical absorption in the film is known.
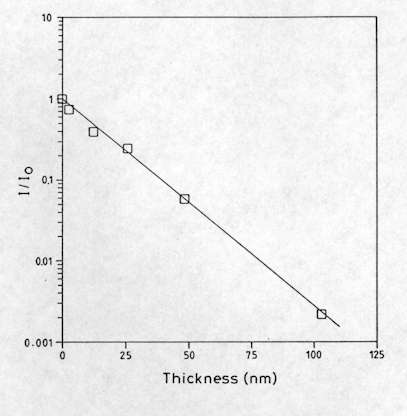
Figure 13. Relative Raman intensity of the first order Si mode in function CoSi2 thickness, recorded on different polycrystalline films.
For amorphous materials, the lack of long-range order yields a breakdown of the momentum conservation rule, and all the phonons become Raman active. For amorphous Si, the spectrum presents four broad bands centred at about 150 cm-1, 310 cm-1, 380 cm-1 and 480 cm-1 (see Figure. 14). It has been shown that the width of the TO mode is a good measure of local order which provides a tool for the structural assessment of the amorphous layers. Further, the quantitative analysis of the band intensities related to the crystalline and amorphous phases gives the crystalline fraction in partially amorphous systems[8].
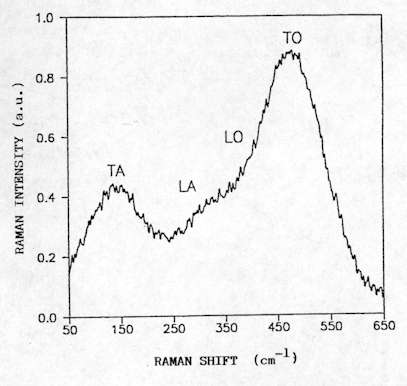
Figure 14. Raman spectrum of amorphous silicon showing the different modes (LO: longitudinal optical, TO: transverse optical,
LA: longitudinal acoustic, TA: transverse acoustic).
High-resolution polarization measurements have also been performed on semiconductors layers in order to determine local crystallographic orientation[17-20]. Free electrical charge carriers (electrons, holes) concentrations in semiconductors have been measured[20-22] in local regions by the analysis of coupled LO-phonon-plasmon modes. These works established that the Raman microprobe is an interesting tool for determining the distribution of the carrier concentration and mobility in III-V compounds, such as GaAs, GaP, GaAlAs, etc., without carrying out electric measurements using electrodes. For highly doped p-type Si, the concentration of carriers can also be determined from the Fano-like deformation of the first order Raman line[11].
Furthermore, interesting information on local temperature in laser mirrors has allowed the optimization of device technology[23-25]. These were determined from the Stokes/anti-Stokes intensity ratio of Raman scattering. This method has also been applied to obtain in a non destructive way local temperature distribution in laser heated microstructures[26,27]. Raman microspectroscopy was also used to analyze semiconductor microstructure fabrication by direct laser writing[28,29], measure dopant activation profiles in GaAs doped with Zn by laser assisted diffusion[30], evaluate change of the crystal quality in molecular beam epitaxial GaAs layers on Si[31], and detect contaminants in integrated circuits[32,33]. Finally, the Raman microprobe has been utilized to get a complete picture of superlattice phonons since the method enables the identification of in-plane interface phonons from the study of their energy dispersion as a function of the in-plane momentum transfer[34,35].
More applications of Raman spectroscopy in the field of semiconductors can be found in references 36 & 37.
Conclusion
We have seen that the capacity of the Raman microspectroscopy has been well exploited in the field of semiconducting materials. It can detect with no sample preparation microinhomogeneities in integrated circuits, defects in both optoelectronic, microelectronic and sensor devices, that are of special technological interest in connection with their possible influence on the device performance. The method also permits quantitative and nondestructive microanalysis of structures and electrical properties in semiconductors. These mainly include damage induced by ion implantation, strains in heterostructures, measurements of crystallographic orientations, polycrystalline grains size and free carriers concentration.
References
- A Pérez-Rodríguez, A. Cornet and J.R. Morante, Microelectronic Eng., 40, 223 (1998).
- T. Jawhari, J.C. Moreno and J.M. Pastor, J. Mater. Sci., 27, 2231 (1992).
- P.M. Fauchet and I.H. Campbell, CRC Crit. Rev. Solid State Mater. Sci., 14, S79 (1988).
- J.R. Morante, J. Samitier and M.S. Benrakkad, Microelectronic J., 27 (1996).
- M.A. Benitez, L. Fonseca, J. Esteve, M.S. Benrakkad, J.R. Morante, J. Samitier and J.A. Schweitz, Sensor and Actuators, A54, 718 (1996).
- M. Furtsch, M. Offenberg, A. Vila, A. Cornet and J.R. Morante, Thin Solid Films, 296, 177 (1997).
- A. Pérez-Rodríguez, Y. Pacaud, L. Calvo-Barrio, C. Serre, W. Skorupa and J.R. Morante, J. Electr. Mater., 25, 541 (1996).
- A. Achiq, R. Rizk, F. Gourbilleau, R. Madelon, B. Garrido, A. Pérez-Rodríguez and J.R. Morante, J. Appl. Phys., 83, 5797 (1998).
- J. Macía, E. Martin, A. Pérez Rodríguez, J. Jiménez, J.R. Morante, B. Aspar and J. Margail, J. Appl. Phys., 82, 3730 (1997).
- J.C. Tsang, P.M. Mooney, F. Dacol and J.O. Chu, J. Appl. Phys., 75, 8098 (1994).
- A. Pérez-Rodríguez, A. Romano-Rodríguez, R. Cabezas, J.R. Morante, T. Jawhari and C.E. Hunt, J. Appl. Phys., 80, 5736 (1996).
- A. Pérez-Rodríguez, A. Cornet, J.R. Morante, J. Jiménez, P.L.F. Hemment, and K.P. Homewood, J. Appl. Phys. 70, 1678 (1991).
- E. Martín, J. Jiménez, A. Pérez-Rodríguez, and J.R. Morante, Mater. Lett., 15, 122 (1992).
- A. Pérez-Rodríguez, J.R. Morante, E. Martín, J. Jiménez, J. Margail, and A.M. Papon, Proceedings of the 5th International Symposium on Silicon-On-Insulator Technology and Devices, St. Louis, Missouri, 1992, pp. 228-236.
- F. Peiró, A. Cornet, J.R. Morante, M. Beck and M.A. Py, J. Appl. Phys., 83, 7537 (1998).
- A. Pérez-Rodríguez, E. Roca, T. Jawhari, J.R. Morante and R.J. Schreutelkamp, Thin Solid Films, 251, 45 (1994).
- J. Sapriel, J. Chavignon, F. Alexandre, P. De Souza, and A.C. Papadopoulo, Inst. Phys. Conf. Ser., 91, 371 (1988).
- G. Kolb, T. Salbert, and G. Abstreiter, J. Appl. Phys., 69, 3387 (1991).
- K. Mizoguchi, and S. Nakashima, J. Appl. Phys., 65, 2583 (1991).
- S. Nakashima, Raman microprobe study of semiconductors, Light Scattering in Semiconductor Structures and Superlattices (D.J. Lockwood, and J.F. Young, eds.), Plenum Press, New York, 1991, p. 291.
- S. Nakashima, H. Yugami, A. Fujii, M. Hangyo and H. Yamanaka, J. Appl. Phys., 64, 3067 (1988).
- M. Herms, G. Irmer, J. Monecke, and O. Oettel, J. Appl. Phys., 71, 432 (1992).
- M.C. Krantz, H.J. Rosen, and W. Lenth, Electron. Lett., 26, 990 (1990).
- G. Abstreiter, Appl. Surf. Sci., 50, 73 (1991).
- W.C. Tang, H.J. Rosen, P. Vettiger, and D.J. Webb, Appl. Phys. Lett. 58, 557 (1991).
- G.D. Pazionis, I.P. Herman, H. Tang, IEEE J. Quantum Electron., 25, 976 (1989).
- H. Brugger, and P.W. Epperlein, Appl. Phys. Lett., 56, 1049 (1990).
- I.P. Herman, D.E. Kotecki, and F. Magnotta, J. Vac. Sci. Technol. a4, 659 (1986).
- I.P. Herman, and F. Magnotta, J. Appl. Phys., 61, 5118 (1987).
- T.J. Licata, D.V. Podlesnik, H. Tang, I.P. Herman, R.M. Osgood Jr., and S.A. Schwarz, J. Vac. Sci. Technol., A8, 1618 (1990).
- A. Ito, M. Ichimura, A. Usami, T. Wada, and H. Kano, J. Appl. Phys. 72, 2531 (1992).
- Y. Hiratsuka, Y. Hirano, and K. Tochigi, Mikrochimica acta, 3, 359 (1984).
- R.Z. Muggli, and M.E. Andersen, Solid State Tecnol., 28, 287 (1985).
- R. Schorer, W. Wegscheider, K. Eberl, E. Kasper, H. Kibbel, and G. Abstreiter, Thin Solid Films, 222, 269 (1992).
- G. Scamarcio, M. Haines, G. Abstreiter, E. Molinari, S. Baroni, A. Fischer, and K. Ploog, Phys. Rev. B Condens. Matter, 47, 1483 (1993).
- S. Nakashima, and M. Hangyo, IEEE J. Quantum Electron., 25, 965 (1989).
- T. Jawhari, “Applications of micro-Raman spectroscopy” in Handbook of Advanced Materials Testing, (N.P. Cheremisinoff ed.), Marcel Dekker, New York (1995).

