Spectroscopic study of the solvation of Tetramethylurea, TMU, in aqueous CH3OD, EtOD, MeCN, DMSO, MeOD-MeCN & MeOD-DMSO solvent systems
Rezaei Behbahani, W. Earle Waghorne
Department of Chemistry,
University College Dublin,
Belfield, Dublin 4,
Ireland
Abstract
Result of studies of tetramethylurea, TMU, in D2O-CH3OD, D2O-EtOD, D2O-DMSO, D2O-MeCN, MeOD-MeCN and MeOD-DMSO mixtures are reported. These data yield information about the composition of the first shell of the –C=O chromophore of TMU in the mixed solvents. It is shown that, for MeOD-MeCN and MeOD-DMSO systems, the composition of the chromophore’s first solvation shell can be reproduced quantitatively by a simple mass action treatment, using only one adjustable parameter. This is the mean equilibrium constant, K*, for the replacement of one component of the mixed solvent by the other in the coordination shell of the chromophore. Calculated and experimental data for aqueous MeOD, EtOD systems don’t fit each other in the entire solvent composition.
Introduction
Infrared spectra of methyl acetate,[1] acetone,[2] and several amides[3, 4] including N, N-dimethylacetamide, in aqueous DMSO mixed solvents, have been reported previously. In mixed solvents, these spectra commonly show several carbonyl stretching bands, which are assigned to differently hydrogen-bonded species.
The spectroscopic measurements show clearly the existence of non-, mono-, and di-hydrogen-bonded –C=O group of TMU in MeOD-MeCN, MeOD-DMSO, aqueous MeOD and EtOD solvent systems. Analyzing of these data allows determination of the proportions of each of these species. In aqueous DMSO and MeCN one single band was found for –C=O stretch but the position of the band shifted to higher values with increasing the aprotic components (DMSO and MeCN in these cases). These measurements provide information about the solvation of –C=O group in TMU.
Experimental and Results
The acetonitrile [5] and DMSO[6] were purified as described previously. Samples of D2O, CH3OD and EtOD were used as supplied by Aldrich. Solutions were prepared by volume using Eppendorf pipettes.
The mid-IR spectra of TMU as the solute were recorded on Mattson 3000 FTIR spectrometer using demountable cells with silver chloride windows. The pathlength was 0.025 cm.
Mid-IR studies of TMU
in mixed solvent systems
The mid-IR spectra of TMU in MeOD-DMSO, MeOD-MeCN and in aqueous methanol and ethanol solvent systems are shown in Figures 1 – 4. In aqueous MeCN and DMSO only one single band was observed with the band position going to higher values with increasing MeCN and DMSO. The results for MeOD-DMSO and MeOD-MeCN solvent systems are consistent with the existence of three species, non-, mono- and di-hydrogen bonded TMU.
There are three bands for TMU in D2O-MeOD and D2O-EtOD systems, corresponding to non-, mono- and di-hydrogen-bonded species.
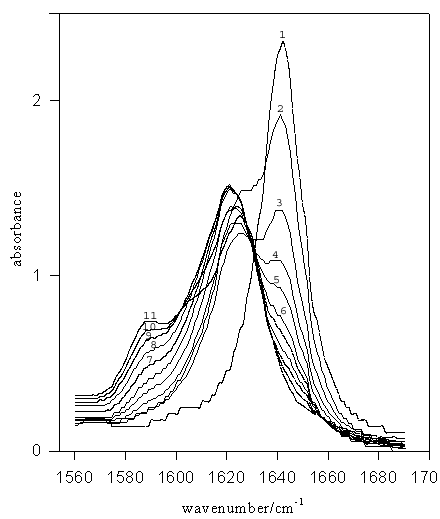
Figure 1. IR spectra for TMU (–C=O stretch) in MeOD-MeCN mixed solvent systems. Mole fractions of acetonitrile are: (1) 1.00 (pure MeCN), (2) 0.9, (3) 0.8, (4) 0.7, (5) 0.6, (6) 0.5, (7) 0.4, (8) 0.3, (9) 0.2, (10) 0.1, (11) pure MeOD.
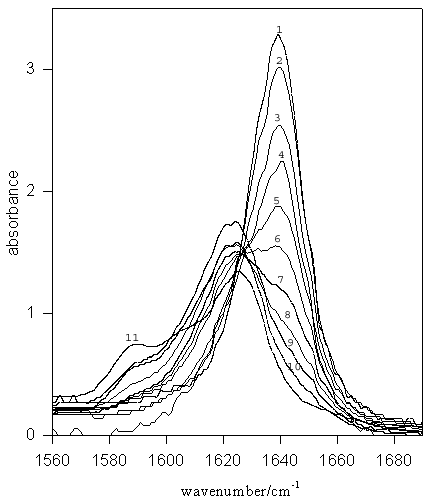
Figure 2. IR spectra for TMU (–C=O stretch) in MeOD-DMSO mixed solvent systems. Mole fractions of DMSO are: (1) 1.00 (pure DMSO), (2) 0.9, (3) 0.8, (4) 0.7, (5) 0.6, (6) 0.5, (7) 0.4, (8) 0.3, (9) 0.2, (10) 0.1, (11) pure MeOD.
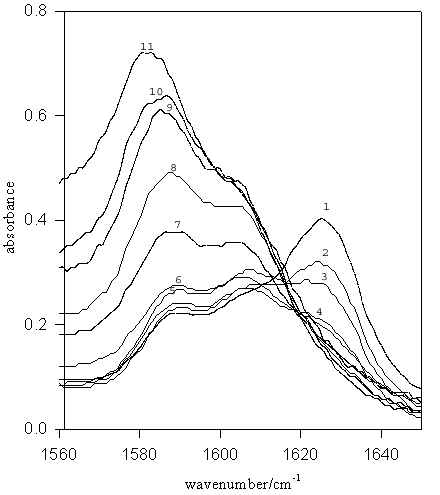
Figure 3. IR spectra for TMU (–C=O stretch) in D2O-MeOD mixed solvent systems. Mole fractions of EtOD are: (1) 1.00 (pure MeOD), (2) 0.9, (3) 0.8, (4) 0.7, (5) 0.6, (6) 0.5, (7) 0.4, (8) 0.3, (9) 0.2, (10) 0.1, (11) pure D2O.
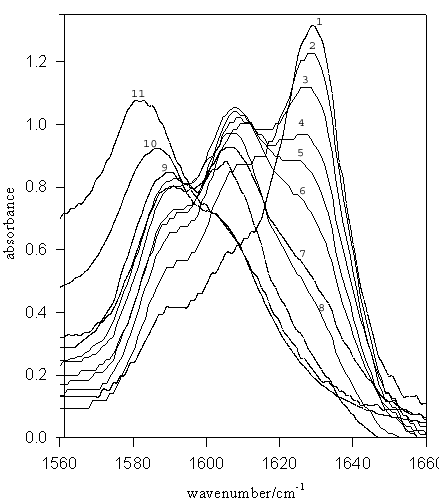
Figure 4. IR spectra for TMU (–C=O stretch) in D2O-EtOD mixed solvent systems. Mole fractions of DMSO are: (1) 1.00 (pure DMSO), (2) 0.9, (3) 0.8, (4) 0.7, (5) 0.6, (6) 0.5, (7) 0.4, (8) 0.3, (9) 0.2, (10) 0.1, (11) pure D2O
Results and Discussion
Solvation is the general term for the attraction and surrounding of solute particle by solvent molecules. When solvation involves organic components the interaction that occurs is generally that of the functional groups of the solute and solvent molecules.
The layer of solvent molecules immediately surrounding the solute molecule in solution is termed the “solvation shell”. Changes in the composition of the solvent will result in change in solvation shell composition. For TMU molecule in aqueous MeCN and DMSO solvent systems, this change in solvent shell composition is reflected in a change in the position of –C=O stretch band in the IR spectra. The carbonyl of free TMU occurs at 1658 cm-1. At higher concentration of protic solvent (i.e. water), the –C=O band occurs at lower wavenumbers. This is expected due to the extent of hydrogen bonding.
Previous study on amides [7] have shown the presence of non-, mono- and di-hydrogen bonded species in mixed solvent system containing at least one hydroxylic component. Three –C=O bands of TMU are observed in the IR spectra corresponding to the three differently hydrogen bonded species in MeOD-MeCN and MeOD-DMSO systems. For N-methylformamide and N, N-dimethylformamide in pure water [7], only the di-hydrogen-bonded species is observed but TMU in pure water, methanol and their mixtures has non-, mono- and di-hydrogen-bonded species, which indicates inductive groups (i.e. –CH3) stabilize the negative charge on the carbonyl Oxygen in amides for making more hydrogen bonds. K1 values, the ratio of the mono- to di-hydrogen-bonded species in pure protic solvent, for TMU in pure MeOD and water (2.3 and 0.65 respectively) show that the formation of di-hydrogen-bonded –C=O species is greater in water, in agreement with the acidity of liquid water (for example the Rechardt ET (30) values of MeOD and water are 55.5 and 63.1, respectively [8]).
Due to steric effect of –CH3 groups, roughly all interactions is related to the solvent with oxygen of –C=O and the interaction with other sites on TMU molecule is almost negligible. Therefore, almost all of changes in mono-/di- and non-/mono- ratios during solvent compositions, correspond to hydrogen bonds of protic solvent with –C=O group.
In the cases of TMU in D2O-MeOD and D2O-EtOD, co-solvents are protic as well and contribute in hydrogen bonding. Not good fitting of experimental data and calculated points is due to the contribution of co-solvent in hydrogen bonding.
We have shown previously [9, 10] that the variation in the relative populations of the differently hydrogen bonded solute species can be accounted for simply in terms of equilibria:
A(H2) ↔ A(H) + H (E1)
A(H) + S ↔ A(S) + H (E2)
A(H2) + S ↔ A(HS) + H (E3)
A(HS) + S ↔ A(S2) + H (E4)
Where A represents the solute and H and S are the mole fraction of protic (water) and aprotic components of the mixed solvent respectively.
The associated equilibrium constants K1 to K4 are given by
![]() (I)
(I)
![]() (II)
(II)
![]() (III)
(III)
![]() (IV)
(IV)
This has been discussed in detail previously [9,10]. Briefly K1 is directly measurable, or can be estimated, from the relative populations of A(H) and A(H2)in pure water. If the solvents H and S are present in a 50:50 ratio (i.e. x=0.5) and if the mean equilibrium constant K* equals 1, then from a statistical point of view, the di-, mono-, and non-hydrogen bonded species would be expected to occur in a 1:2:1 ratio.
![]()
1 : 2 : 1
The equilibrium constant, ![]() and
and ![]() , would be then related statistically such that:
, would be then related statistically such that:
![]() and
and ![]() (2)
(2)
Where K* is the mean equilibrium constant and so ![]() . The number of adjustable parameters is reduced further by setting
. The number of adjustable parameters is reduced further by setting ![]() equal to
equal to ![]() , which corresponds to the approximation that the solute hydrogen bond energies are equal in mono-hydrogen-bonded species A(H) and A(HS).
, which corresponds to the approximation that the solute hydrogen bond energies are equal in mono-hydrogen-bonded species A(H) and A(HS).
Thus only one adjustable parameter, K*, is required to fit the data. The values of K1, K2=K4 and K3 obtained by fitting the experimental data to the above equilibrium scheme are listed in Table 1 and the calculated and experimental variation in the relative populations of the di-, mono- and non-hydrogen bonded (the latter two as the sums of A(H) and A(HS), and A(S) and A(S2), respectively) are compared in Figures 5-10. The agreement between the calculated and experimental values is satisfactory, for the MeOD-MeCN and MeOD-DMSO systems; however, it was not possible to fit the data for the aqueous MeOD, EtOD systems to this simple model.
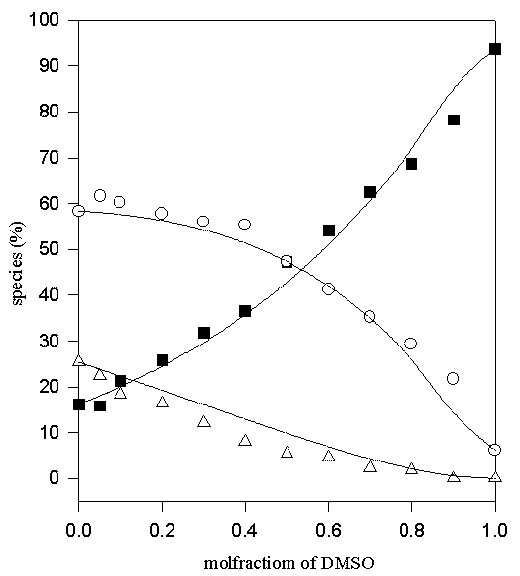
Figure 5. Comparison of experimental (symbols) and calculated (lines) values of the percentage non- (♦), mono- (O) and di-hydrogen-bonded (Δ) TMU in MeOD-DMSO solvent system
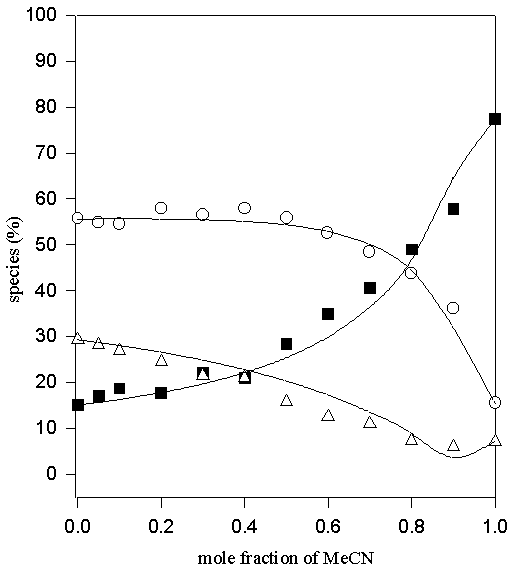
Figure 6. Comparison of experimental (symbols) and calculated (lines) values of the percentage non- (♦ ), mono- (O) and di-hydrogen-bonded (Δ) TMU in MeOD-MeCN solvent system
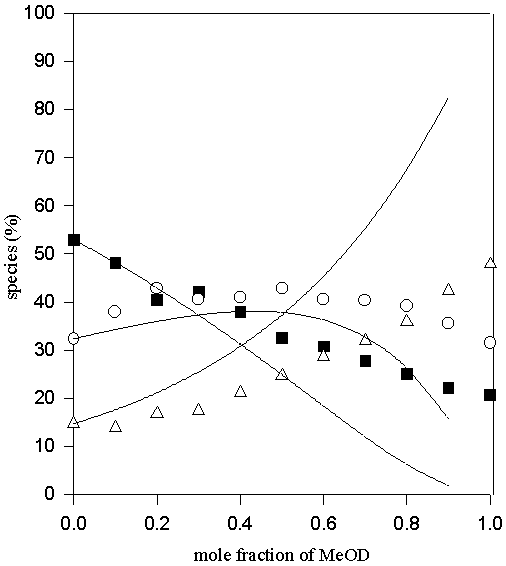
Figure 7. Comparison of experimental (symbols) and calculated (lines) values of the percentage non- (♦ ), mono- (O) and di-hydrogen-bonded (Δ) TMU in D2O-MeOD solvent system
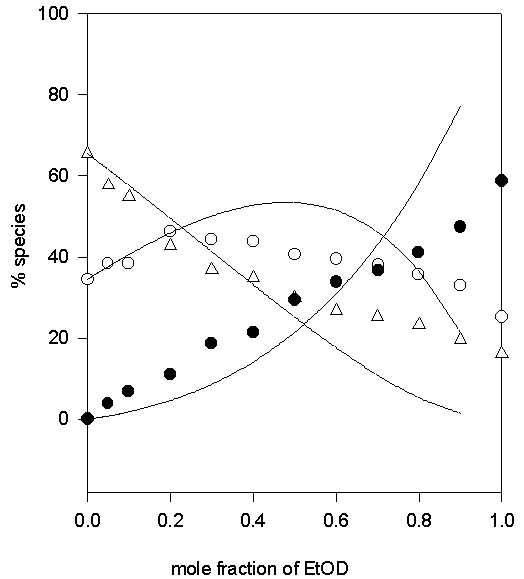
Figure 8. Comparison of experimental (symbols) and calculated (lines) values of the percentage non- (♦), mono- (O) and di-hydrogen-bonded (Δ) TMU in D2O-EtOD solvent system
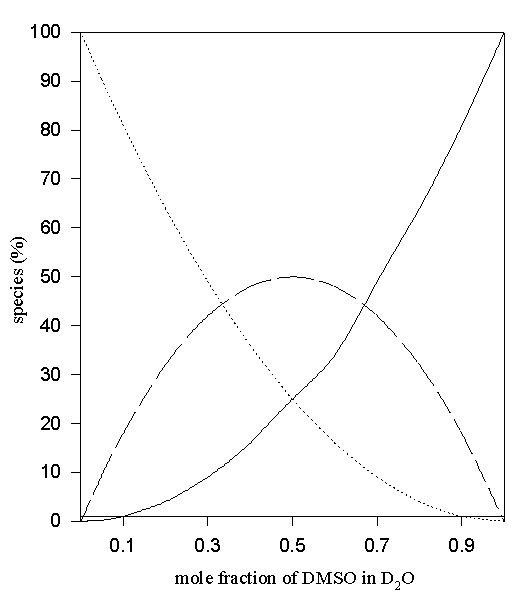
Figure 9. Predicted values of the percentage non- (solid line), mono- (—-) and di- hydrogen-bonded (…..) TMU in D2O-DMSO solvent system via eqn. 4.
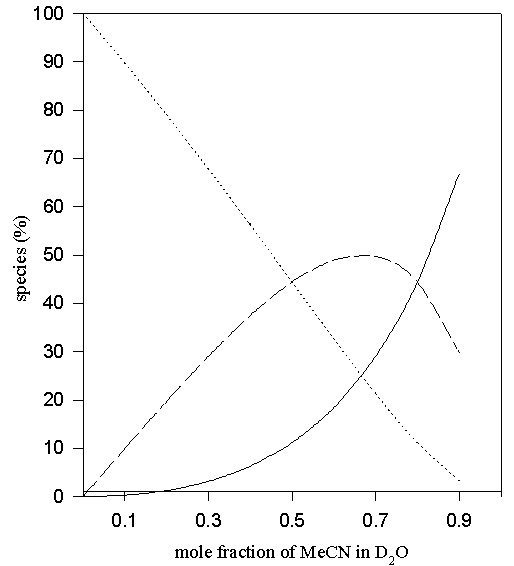
Figure 10. Predicted values of the percentage non- (solid line), mono- (—-) and di-hydrogen-bonded (…..) TMU in D2O-MeCN solvent system via eqn. 4.
The situation is different for aqueous acetonitrile and DMSO, since no separate peaks are observed for the differently hydrogen bonded in these systems. If we assume that the shift in the –C=O band reflects changes in the composition of its solvation shell, then we can write:
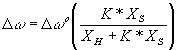 (4)
(4)
Where ? ? is the change in the band position (in wave numbers) from water to the mixed solvent and ? ? o is the change from water to DMSO or MeCN. ![]() and
and ![]() are mole fraction of aprotic (DMSO and MeCN in this case) and protic solvent respectively.
are mole fraction of aprotic (DMSO and MeCN in this case) and protic solvent respectively.
In the case of aqueous DMSO and MeCN eqn. (4) was used to predict the percentages of di-, mono- and non- hydrogen-bonded species. Predicted points for these systems are shown in Figures 9 – 10.
Where both solvent components are protic, as is the case for the aqueous
methanol and ethanol, the additional equilibrium:
A(S) + S ↔ A(S2)(5)
With: ![]()
![]()
Must be taken into account; however this case is simplified, since:
![]()
In all cases the value of ![]() (or )
(or ) ![]() can be determined simply from the proportions of the mono- and di-hydrogen-bonded species present in the protic (or aprotic) component.
can be determined simply from the proportions of the mono- and di-hydrogen-bonded species present in the protic (or aprotic) component.
![]()
The values of ![]() provide straightforward information about preferential solvation of the solute chromophore. Thus
provide straightforward information about preferential solvation of the solute chromophore. Thus ![]() <1 indicates preferential solvation by the protic component, H2O, and
<1 indicates preferential solvation by the protic component, H2O, and ![]() >1 preferential solvation by the aprotic component, clearly
>1 preferential solvation by the aprotic component, clearly ![]() equal to unity represents random solvation.
equal to unity represents random solvation.
| Table 1. Values of |
|||||
| Solvent system | |||||
| D2O-MeCN | 0.65 | 0.25 | 1.0 | 0.25 | 0.5 |
| D2O-MeOD | 0.65 | 0.1 | 0.4 | 0.1 | 0.2 |
| D2O-EtOD | 0.65 | 0.1 | 0.4 | 0.1 | 0.2 |
| D2O-DMSO | 0.65 | 1.1 | 4.4 | 1.1 | 2.2 |
| MeOD-DMSO | 2.31 | 0.63 | 2.5 | 0.63 | 1.25 |
| MeOD-MeCN | 2.31 | 0.2 | 0.8 | 0.2 | 0.4 |
It is interesting to note that, while K* for TMU are less than unity, indicating preferential solvation by water that for D2O-DMSO is larger than unity. Preferential hydration of the basic TMU –C=O group is reasonable, since its interaction with the water –O–H protons is expected to be stronger than those with the aprotic molecules.
References
- K.B. Patel, G. Eaton, & M.C.R. Symon, J. Chem. Soc. Faraday Trans. I, 85, 2775(1985).
- M.C.R. Symon & G. Eaton, J. Chem. Soc. Faraday Trans. I, 81, 1963 (1985).
- G. Eaton, & M.C.R. Symon, J. Chem. Soc. Faraday Trans. I, 84, 3429 (1988).
- G. Eaton, & M.C.R. Symon, & P.P. Rastogi, J. Chem. Soc. Faraday Trans. I, 85, 3257 (1989).
- C. Cronnolly, K.C. Pillai, & W.E. Waghorne, J. Electroanal. Chem. 207, 177 (1986)
- B.G. Cox and W.E. Waghorne, J. Chem. Soc. Faraday Trans. I, 80, 1267 (1984).
- J.G. Kirkwood and F.P. Buff, J. Chem. Phys. 19, 774 (1951).
- J. Burgess, Metal Ions in Solution, Ellis Horwood, Chichester, 32 (1978)
- K.E. Newman, J. Chem. Soc. Faraday Trans. I, 84, 1387 (1988).
- W.E. Acree, Fluid Phase Equilibria 92, 19 (1994).
Received 18th February 2002, accepted 4th March 2002.
REF: G.R. Behbahani, W.E. Waghorne, Int. J. Vib. Spect., [www.irdg.org/ijvs] 6, 2, 5 (2002)

