On the use of Neutron Inelastic Scattering and DFT Calculations to test the Reliability of the Force Fields for Nucleic Acid Building Blocks
Hervé Jobic1 and Mahmoud Ghomi2*
1Institut de Recherche sur la Catalyse,
2 Avenue A. Einstein,
69626 Villeurbanne,
France.
2Laboratoire de Physicochimie Biomoléculaire et Cellulaire,
UMR 7033,
Université Pierre et Marie Curie,
Case courrier 138,
4 Place Jussieu,
F-75252 Paris Cedex 05,
France.
E-mail: ghomi [at] lpbc.jussieu.fr
Keywords
uracil, uridine, cytosine, cytidine,
nucleic acids, RNA, DFT calculations,
neutron inelastic scattering,
vibrational spectra, force field, molecular modeling.
Abstract
Neutron inelastic scattering (NIS) spectra of nucleic acid building blocks (bases, nucleosides, nucleotides) are recorded in the solid phase at a cryogenic (T=15 K). An attempt to interpret these spectra has been made by a harmonic force field obtained at the DFT/B3LYP/6-31G* level.
Introduction
Nucleic acids (DNA: Deoxyribonucleic Acid and RNA: Ribonucleic Acid) are linear polymers which take part in many biological processes, such as transcription, translation, replication and catalysis. The analysis of the structural properties of these molecules may help to understand their functions. DNA generally adopts right- or left-handed double helical conformations, whereas, RNA is a single stranded molecule which can be present in a variety of complex secondary and tertiary structures, through the formation of intramolecular double helices and hairpins. A nucleic acid strand is formed by the repetition of nucleotides. A nucleotide is composed of a base (uracil in RNA, thymine in DNA, and cytosine, guanine and adenine in both DNA and RNA), a sugar (deoxyribose in DNA and ribose in RNA) and a phosphate group. Nucleosides (base+sugar) are also important building blocks of nucleic acids. They can adopt C3’-endo/anti, C2′-endo/anti and C3′-endo/syn conformations depending on the global structure of the nucleic acid strand in which they are involved. We recall here that C2’-endo and C3’-endo refer to the sugar conformations, and anti and syn correspond to the orientation of the base with respect to the sugar [1].
The analysis of the vibrational spectra of the nucleic acid building blocks can help to understand their structural features. The vibrational motions analysed by optical spectroscopy (Raman scattering and infrared absorption) are generally those arising from the heavy atom (C, N, O and P) vibrational motions. Taking into account the large value of the hydrogen inelastic cross section in the neutron innelastic scattering (NIS) process, the most intense bands arise from the vibrational modes which involve the hydrogen motions. This particular behaviour allows a better analysis of the C-H and N-H out-of-plane wagging motions of the bases as well as the characteristic vibrational modes of the sugar, which are incompletely analysed by optical vibrational spectroscopy. On the other hand, obtaining a reliable molecular force field is also challenging in biomolecular modelling. In fact, molecular mechanics and dynamics simulations on DNA and RNA structures need geometric parameters, atomic charges and force constants of nucleosides and nucleotides. All these parameters can be obtained by theoretical calculations on the basis of vibrational spectral data. NIS spectra are extremely valuable to achieve this goal. We have chosen the density functional theory (DFT) method which introduces the exchange-correlation effects by means of appropriate functionals, in order to analyse both the geometric and vibrational features of nucleic acid constituents.
To date we have recorded and calculated the NIS spectra of all the major nucleic acid bases and nucleosides. To give an example of the whole set of our work on the subject, we report here those results concerning two nucleosides involved in the RNA structure, i.e. uridine and cytidine.
Experimental and theoretical details
Figure 1 displays the chemical structure of the nucleosides reported in this paper. Powder samples of the bases and nucleosides and species with labile hydrogens deuterated have been used. Analysed samples correspond to polycrystalline states and not to amorphous ones. NIS spectra of the bases as well as uridine have been recorded at T=15 K on dry samples on the TFXA spectrometer at the Rutherford-Appleton Laboratory (United-Kingdom), whereas the spectra of all other nucleosides were recorded on the IN1-BeF spectrometer (T=15 K) installed at the Institut Laue-Langevin (Grenoble, France). The TFXA spectrometer is a time of flight instrument with an inverse geometry and a time-focusing analyser; it has good energy transfer resolution (D E/E» 2%) over a wide range of energy transfers. The accuracy on the band positions is about ± 10 cm-1. The IN1-BeF spectrometer has a beryllium filter placed between the sample and the detector. This setting gives a moderate energy resolution, the instrumental resolution varying from 25 cm-1, at low energy transfers, to 50 cm-1at large energy transfers. The estimated absolute accuracy is of ± 15 cm-1. A better resolution can be obtained on IN1-BeF, using an additional graphite filter, but at the expense of the signal intensity [2]. The neutron-transmission of the different samples was about 90% so that multiple scattering effects can be neglected.
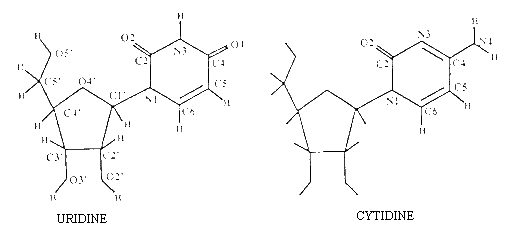
Figure 1. Chemical structure and atom numbering
of uridine and cytidine
To establish a molecular force field by means of the DFT method we used the B3LYP functional [3-4] 6-31G* valence split atomic orbital basis sets containing d polarisation orbitals on heavy atoms (C, N, O). Harmonic vibrational modes have been calculated after a full geometry optimisation of each molecular compound. All quantum mechanical computations, i.e. geometry optimisation and harmonic force field calculations (estimated by the second derivatives of the molecular energy with respect to the atomic cartesian coordinates) have been performed by using a Gaussian package [5]. For vibrational calculations with optimised geometry and quantum mechanical harmonic force field as input, home-made program BORNS. This program provides the harmonic force constants in terms of internal coordinates, redundancy removal, as well as the calculation of vibrational wavenumbers and atomic displacements and the assignment of the calculated modes in terms of the potential energy distribution (PED) matrix elements. To calculate NIS spectra, only the first-order spectra arising from the interaction of the incident neutron with only one internal vibrational quantum, has been taken into consideration. The simulation of the spectra is based on the Zemach and Glauber formalism [6], it only requires the frequencies and atomic displacements [2]. We have verified that in the case of nucleic acid bases, the higher-order NIS spectra (arising from the interaction of the neutron with several vibrational quanta) give rise to a continuous background superimposed upon the first-order NIS spectra, rather than to additional new peaks (phonon-wings). This is due to the large effective mass of the molecules considered. The background due to multiphonon excitations explains the difference in the baseline observed between experimental and simulated spectra, especially at large energy transfers (On both the TFXA and IN1-BeF spectrometers, the energy transfer is proportional to Q2, since the intensity of multiphonon processes of order n is propotional to (Q2)n, the intensity rises with increasing energy transfer). In order to give a continuous shape to the calculated spectra, a gaussian band profile has been selected whose maximum intensity corresponds to the calculated NIS intensity of a given vibrational mode, whereas its half-width is fitted to the instrumental resolution of the spectrometers used (see above). No scaling factors have been applied to correct the calculated harmonic force constants in order to improve the agreement between the calculated and observed results (wavenumbers and NIS intensities).
Results and Discussion
Geometry optimisation of the bases and nucleosides has revealed the following main results: (i) uracil gives rise to a perfect planar configuration belonging to the Cs point group. (ii) in cytosine, guanine and adenine a non-planar (pyramidal) amino group (NH2) configuration has been found upon geometry optimisation with energetically a double minimum character corresponding to the orientation of this group toward one side or the other of the base plane. The pyramidal conformation of the NH2 group is a consequence of sp3 hybridisation and has been mentioned in several recent papers based on the geometry optimisation of nucleic acid bases at different theoretical levels (with or without consideration of the correlation effect) [7-10]. (iii) in nucleosides, the junction of the sugar to the base through the glycosyl linkage also leads to a slight non-planar deformation of the base atoms. To analyse the NIS spectra of nucleosides recorded on polycrystalline powder samples, we have only considered those conformers which correspond to the crystal X-ray diffraction patterns of these compounds, for instance the C3’-endo/anti conformers in uridine [11] and cytidine [12]. The calculated NIS spectra of the nucleosides and their deuterated species are displayed in Figures 2 and 3, respectively, and compared with the observed ones in the same spectral region (0-2000 cm-1). Comparison between the observed NIS spectra obtained from the bases and its parent nucleosides clearly shows the vibrational modes arising from the ribose moiety are located mainly in the following wavenumber regions: 1500-1200 cm-1, 1000-950 cm-1, 700-600 cm-1 and below 500 cm-1.
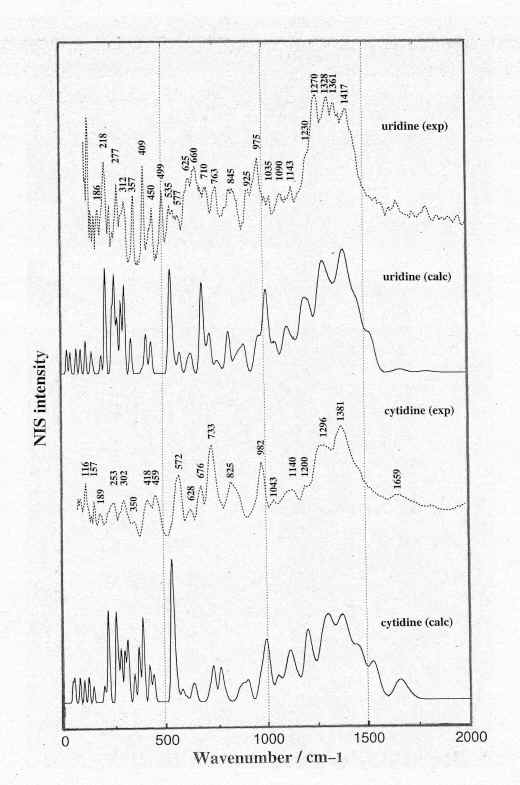
Figure 2: Comparison between the observed (solid line)
and calculated (dotted line) NIS spectra of uridine in the
spectral region below 2000 cm-1.
The relative differences between the calculated and observed wavenumbers in the 2000-900 cm-1 spectral region do not exceed 3%. The main reason for this agreement is that the vibrational modes located in this region are barely affected by intermolecular H-bonds in solid phase. The analysis of the vibrational modes arising from the ribose moiety in uridine [20] allowed us to confirm that: (i) the intense and partially resolved bands in the 1200-1500 cm-1 region, are basically assigned to the CH2, N-C-H, O-C-H and C-C-H angular bendings of sugar ring. (ii) the less intense resolved bands appearing in the 700-600 cm-1 range and below 500 cm-1 can be assigned to the angular bendings and torsional motions of ribose.
The same spectral features as mentioned above can also be emphasised in the case of cytidine. The main discrepancies are generally located in the spectral region below 900 cm-1, where they are found in an increasing order from uridine to cytidine (Figure 2). We should state that the ribose moiety (Figure 1) in the presently studied nucleosides has the same number of possible sites for intermolecular H-bonding, i.e. the three hydroxyl groups located in the 2’, 3’ and 5’ sites. Thus, the vibrational modes of ribose should be affected in the same manner by possible intermolecular H-bonding in the condensed phase. Consequently, their different behaviour as far as the comparison between their calculated and observed NIS spectra is concerned, should primarily arise from the nature of the base included in their chemical structure.
In order to test our assumptions on the solid phase H-bonding effects, we have recorded and calculated the NIS spectra of their analogues deuterated species on their labile hydrogens (Figure 3). A better agreement is thus found upon deuteration between the observed and calculated NIS spectra in the whole spectral region below 2000 cm-1. Due to the much smaller incoherent cross section of deuterium compared with that of hydrogen, the NIS bands in which labile hydrogens participate, vanish upon deuteration and the agreement between the calculated and observed results is consequently improved.
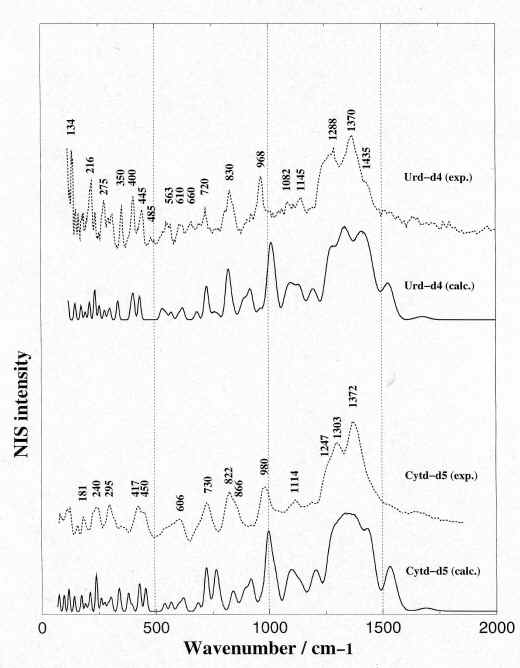
Figure 3. Comparison between the observed (solid line)
and calculated (dotted line) NIS spectra of deuterated
species of uridine and cytidine.
Urd-d4 is the deuterated species of uridine on the four
labile hydrogens located on N3, O2′, O3′ and O5′ atoms.
Cytd-d5 is the deuterated species of cytidine on the five
labile hydrogens located on N4, O2′, O3′ and O5′ atoms.
See Figure 1
In conclusion, the discrepancies observed when comparing the experimental and theoretical NIS spectra of bases and nucleosides, is mainly related to the intermolecular effects existing in the condensed phase and not to any insufficiency of the theoretical level, i.e. the DFT level [13-14]. Recently, more realistic calculations based on an uracil surrounded by two water molecules (forming intermolecular H-bonds on the N1 and N3 sites) and mimicking the possible intermolecular H-bonds in the solid phase [15-16], revealed a considerable upshift of the N1-H and N3-H wagging modes to 797 cm-1 and 859 cm-1, respectively, i.e. very close to the corresponding observed NIS peak observed in the solid phase (˜831 cm-1). The same situation also occurs in the case of cytosine as shown by our recent theoretical calculations on this base surrounded by water molecules (results to be published).
Acknowledgements
We thank the staff of the Institut Laue-Langevin (Grenoble, France) and the Rutherford-Appleton Laboratory for their technical assistance in using the IN1-BeF and TFXA spectrometers, respectively. Dr. J. Tomkinson and Dr. A. Ivanov are particularly acknowledged. The authors thank IDRIS (CNRS, Paris), CINES (Montpellier) and CCR (University Paris 6) for access to their computational facilities.
References
-
W. Saenger, Principles of Nucleic Acid Structure, Dd. C. R. Cantor, Springer-Verlag, New York (1984).
-
H. Jobic and H.J. Lauter, J. Chem. Phys. 88, 5450 (1988),.
-
R. G. Parr and W. Yang, Annu., Rev. Chem. 46, 701 (1995).
-
A. St-Amant, Density Functional Methods in Biomolecular Modeling, Reviews in Computational Chemistry, Vol. 7, Eds. K. B. Lipkowitz and D. B. Boyd, VCH Publishers Inc., New York (1996).
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C.Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K., A. D. MalickRabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle and J. A. Pople, Gaussian, Inc., Pittsburgh PA, (1998).
-
A. C. Zemach and R. J. Glauber, Phys. Rev., 101, 118 (1956)
-
J. S. Kwiatkowski, J. Leszcynski, J. Phys. Chem., 100, 941 (1996).
-
D.A. Estrin, L. Paglieri, G. Corongiu, J. Phys. Chem., 98, 5653 (1994).
-
J. Sponer, J. Leszczynski, P. Hobza, J. Biomol. Struct. Dyn., 14, 117 (1996).
-
J. Smets, L. Adamowicz and G. Maes, J. Phys. Chem., 100, 6434 (1996).
-
E. A. Green, R. D. Rosenstein, R. Shiono, D. J. Abraham, B. L. Trus and R.E. Marsh, Acta Cryst. B. 31, 102 (1975).
-
S. Furberg, C.S. Petersen and C. Romming, Acta Cryst., 18, 313 (1965).
-
N. Leulliot, M. Ghomi, H. Jobic, O. Bouloussa, V. Baumruk and C. Coulombeau, J. Phys. Chem. B., 103, 10934 (1999).
-
M.P. Gaigeot, N. Leulliot, M. Ghomi, H. Jobic, C. Coulombeau and O. Bouloussa, , Chem. Phys., 261, 217 (2000).
-
M. Ghomi, A. Aamouche, B. Cadioli, G. Berthier, L. Grajcar and M. H. Baron, J. Mol. Struct., 411, 323 (1997).
-
A. Aamouche, G. Berthier, B. Cadioli, E. Gallinella and M. Ghomi, J. Mol. Struct. (THEOCHEM), 426, 307 (1998).
Received 12th July 2001, received in revised format 2nd August 2001,
accepted 2nd August 2001.
REF: H. Jobic & M. Ghom Int. J. Vib. Spect., [www.irdg.org/ijvs] 5, 4, 5 (2001)

