Hot Samples in Raman Spectroscopy
The Editor
From the earliest days in the development of Raman spectroscopy it was appreciated that it was very easy to examine samples at high temperatures. When Mercury discharge lamps were the source of choice it was hard to examine powders but liquids and melts were much easier. When the laser came along in the 1960’s, nothing much changed except that it became much, much easier to build heated cells for use with a laser and of course, the spectra were a good deal better.
Some people went to quite extreme conditions. For example I remember Ian Beattie at Southampton and his group studying molten inorganic materials using He/Ne and later Ar+ sources in the 1960’s and early 1970 showing that Group III halides found as M2X6 in the solid state became M+MX4– in the melt. Ian used quartz cells electrically heated and Spex or Cary 82 Raman instruments.
Now, as you raise the temperatures of a sample it increasingly emits so-called blackbody radiation. By the time you reach ~ 600° some of this emission is in the visible – the sample is red hot. The equation governing the black body emission is –
The blackbody emission LB (λ, T)dλ = (2hc2 / l 5) x exp (hc/lkT –1)-1d λ
in watts, metres-2, steradians-1
where :-
h = Planck’s Const.
c = Vel. of light
l = wavelength
k = Boltzmann Constant
T = Temperature
Hence it turns out that if you are using red or green excitation (remembering that for all practical purposes one is ‘always’ operating on the Stokes side of the existing line) the sample emission becomes obtrusive by 700° C. Clearly, this is not a problem if ones’ aim is to study organics or polymers when temperatures between ambient and 300° C are required but molten salts or molten inorganics are a different matter. They may well need heating to 1000° C or more. See Figure 1.
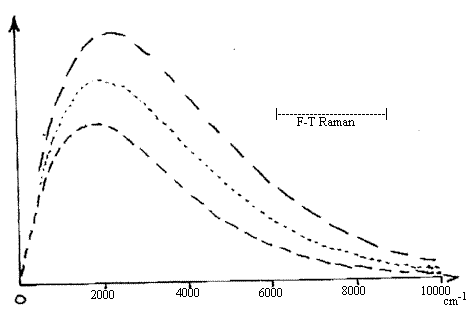
Figure 1. Blackbody emission curves for an emitter at 200K
(top spectrum), 1800K and 1600K (bottom spectrum).
Note that as the temperature rises the strength
of the emission rises at all frequencies and that
the maximum moves to higher frequencies.
Visibly excited Raman spectra lie to the right of
the plots. F-T Raman spectra excited by
the NdYAG laser lie in the indicated domain.
Fortunately, there is a way of discriminating the sample emission from the Raman scattering – phase sensitive detection. If the source (laser) is interrupted with an electronic or mechanical chopper at frequency ν chop the Raman radiation, which is essentially instantaneously excited will appear at this frequency and exactly in-phase with the chopper. The sample emission will be continuous, see Figure 2. The detector (usually a photo-multiplier) out-put is then fed through a phase-sensitive detector an electronic device which is tuned to look for the chopped rather than the continuous signal and hence the Raman spectra can be detected against a heavy emission background. That the method works is perhaps best demonstrated by the Raman spectra of flames! Back in 1971 we had a look at flames and were able to discriminate between the Raman spectra of the gases within the flame (CH4, CO, CO2, N2 etc) and the very intense emission from the flame itself. See Figure 3.
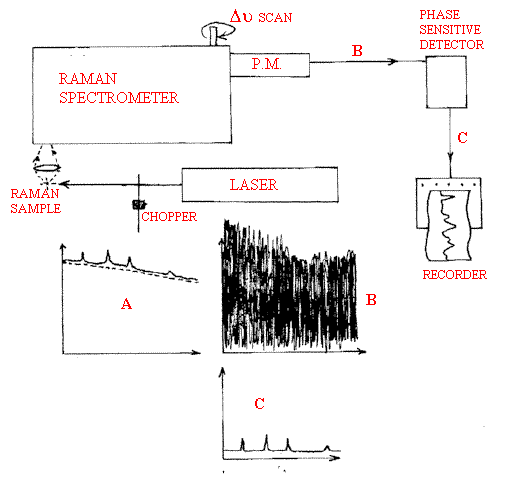
Figure 2
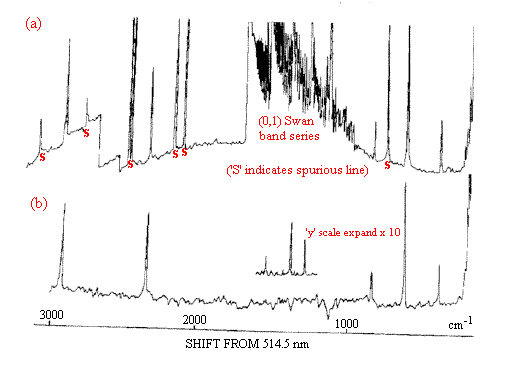
Figure 3. Spectrum (a) is that of the flame plus the Raman experiment.
The bands marked S are the lines due to the flame emission
and the background is also due to the flame.
After passing the signal through a phase sensitive detector, we get spectrum (b).
Now, only the Raman bands appear.
Identification (partial): Swan bands are due to C2 radicals
in the hydrocarbon/air flame.
~2900 cm-1 CH4
~2300 cm-1 N2
Series ~800/600/400 Rotational bands due to H2
Nowadays UV, visible and deep red spectra are almost invariably detected using CCD detectors. Although the technology exists to make these devices discriminate between AC and DC signals, it is complex and rarely encountered hence most current Raman systems do not have the facilities to discriminate against backgrounds. On the other hand, they do have very considerably enhanced sensitivity versus their historical counterparts based on photo-multipliers. It is possible to trade-off this sensitivity against discrimination but the results don’t really compare with the old methods. The logic is explained in Ref 1, however the point to remember is that if you need to examine a heated sample with a visible instrument you are OK up to 600° C or so. As a result, no problem is encountered with organics and polymers.
Fourier Transform Raman
The emission problem in F-T Raman spectroscopy is identical to that in the visible. The problem is much more severe because in F-T Raman we use a near infrared laser source. The normal source is the NdYAG laser operating at 1.064μ (9398 cm-1) hence the spectrum lies between 1.064 and 1.7μ (9398-5800 cm-1). If you apply equation 1 you then find that severe emission will appear at Δν = 3000 cm-1 or 1.7μ at temperatures as low as 160° C not 600° C when using a green source. 160° C is a bit low for many applications. Although polyethylene and polypropylene melt below 200° C many others don’t, many pure organics melt or undergo interesting phase transitions between 200 and 300° C. Many dehydration or irreversible chemical transitions don’t occur below 200° C so users of F-T Raman complain a great deal about sample emission.
The spectrum of a thermally emitting sample shows a high background at high shifts falling steadily towards the exciting frequency. See Figure 4 You might think it is OK to study Raman spectrum over the smooth background. Since the formula of this background follows a well-defined equation you could arrange to subtract it. The problem is noise. The noise in an F-T derived spectrum is proportional to the energy in the total spectrum (including of course, the background). As a result, as the sample is heated, the noise gets much worse and hence you lose sensitivity.
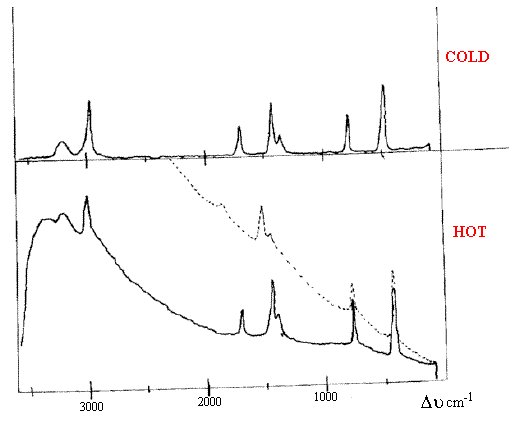
Figure 4. 2 Schematic spectra of the same compound –
one recorded at room temperature, the other at around 180°C.
Above 200°C the background becomes overwhelming –
see dotted spectrum and typically the electronics fail to
cope with the intensity i.e. no spectrum is recorded.
Problems should be tackled, as we all know. The simplest method is to use a filter to drastically attenuate the background. If you insert a filter cutting out radiation to the red of 7398 cm-1 you can remove most of the blackbody emission yet still see the Raman bands from Δν = 2000 → 0 cm-1. You lose the hydrogenic stretches but keep the rest. Using such a filter you can then wind up the temperature to around 275 ºC. See Figure 5. There are other things you can do.
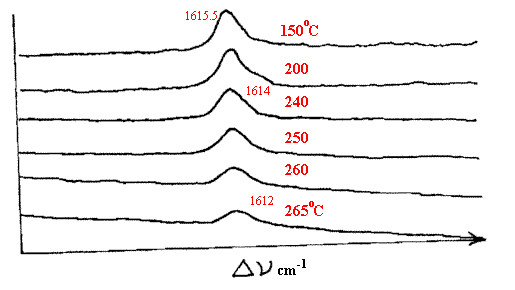
Figure 5. Taken from A. Brookes et al. Spectrochim Acta A 53 (1997) 2313-2321. A series of spectra of polyethylene terephthalate.
As the temperature is raised, the νc=0 band moves to lower frequencies.
Spectra of several other polymers are shown in this paper
recorded at temperatures up to 265°C.
Phase sensitive detection is feasible in F-T Raman but you must chop at a very high frequency. David Cutler and colleagues at Perkin Elmer, UK showed the feasibility of doing this [2]. The problem is that a detector and its electronics optimised to record F-T spectra will be set up to span the frequency range up to only 5Khz. If the chopper is to run at say 25 KHz then the performance of the detector/electronics has to be compromised.
There is another very clever way of doing the job, a technique developed and described by Bob Bennett again at Perkin Elmer, UK [3].
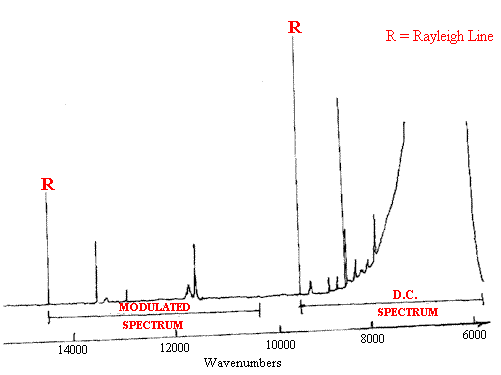
Figure 6. The F-T Raman spectrum of heated polystyrene recorded with a modulated laser. The spectrum is taken from ref.3 (but simplified).
The modulation of the laser offsets the ‘modulated spectrum’ by +5260cm-1.
The DC spectrum complete with its blackbody derived background
plus the UP shifted modulated spectra are shown.
Note that the offset spectrum has no background.
There is no spectrum in the deep red between 12000 and 14000 cm-1.
The frequency scale accommodates the 5260cm-1 offset which is purely a mathematical function.
The interferometer scans and generates an interferogram. The plot is signal vs. optical delay. As the delay is scanned, the signal appears as an AC function with a frequency domain lying between zero and 5000 hz (in a sense this statement is not accurate because the frequency range depends on both the wavelength of the radiation AND the scan speed. The range I quote is typical of current practice). If the laser is sinusoidally varied in intensity at an intermediate frequency – say 500 hz then mixing occurs and three interferograms are produced – the normal one and two others shifted upwards or downwards in frequency by 500hz. If the sample is emitting (a continuous process) only the central one contains information about the emission, the shifted ones ignore the emission. In Figure 6, I show a spectrum taken from Bob’s paper. As you see, it really works. Oddly however, the instrument manufacturers haven’t taken it up and to my knowledge no-one currently offers the kit and software to take advantage of what seems to me a really clever idea.
References
- P.J. Hendra, C. Jones & G. Warnes, F-T Raman Spectroscopy, Ellis Harwood 1991, Chichester UK. Pages 66-72.
- D.J.Cutler & C.J. Petty, Spectrochim. Acta 50A, 1159 (1994).
- R. Bennett, Spectrochim. Acta 50A 1813 (1994)
REF: P.J. Hendra, Int. J. Vib. Spect., [www.irdg.org/ijvs] 5, 3, 4 (2001)

