Conformational and Vibrational Analysis of N-3-Pyridinylmethanesulfonamide
N-3-Pyridinylmethanesulfonamide
Nicolay I. Dodoff
Institute of Molecular Biology,
Bulgarian Academy of Sciences,
Acad. G. Bonchev Street,
Block 21, 1113 Sofia,
Bulgaria
E-mail: dodoff [at] bas.bg
Abstract
Conformational modelling of the molecule of N-3-pyridinylmethanesulfonamide has been performed by the molecular mechanics method. An HF ab initio (3-21G(*) basis set) optimization for the lowest-energy conformation thus obtained has also been carried out, followed by a calculation of the fundamental vibrations. The IR spectrum (4000-150 cm-1) of the compound has been studied in the solid state and in CCl4 solution. An assignment of the IR spectrum has been performed taking into account the results of the ab initio vibrational analysis. A significant low-frequency shift of the NH stretching vibration has been noted in the spectrum of the crystalline compound as compared to the solution one. The existence of an intermolecular hydrogen bond involving the pyridine nitrogen atom and the hydrogen atom of the sulfonamide group has been suggested.
Key word
N-3-Pyridinylmethanesulfonamide, IR spectra, Conformations, Molecular mechanics, HF ab inito calculations.
Introduction
Recently, we studied the conformational behaviour and vibrational spectra of methanesulfonylhydrazine [1] and some of its azomethine derivatives [2, 3]. Our interest in methanesulfonamide derivatives was inspired by fact that compounds of this class possess versatile pharmacological activity, and, in particular, anti-tumor effects [4-6]. Mesitylated aminopyridines could also be of interest in this direction, moreover because they resemble some of the structural fragments of Amsacrine, a pronounced anticancer agent [4]. They should also exhibit complex-forming properties toward metal ions, although their coordination ability seems not to have been explored. Recently we prepared a series of platinum group metal complexes of N-3-pyridinylmethanesulfonamide (PMSA) with expected cytostatic activity, and this work is currently in progress. For the characterization of these metal complexes, the detailed assignment of the infrared (IR) spectrum of the ligand itself is necessary. Such data were however not found in the literature.
Here we wish to report the molecular mechanics (MM) conformational analysis of PMSA and the assignment of its IR spectrum supported by Hartree-Fock (HF) ab initio calculations of the fundamental vibrations.
Experimental
Starting materials and solvents were commercial products (purum or pro analysi.). When necessary, the solvents were purified according to routine procedures [7].
PMSA was synthesized from methanesulfonyl chloride and 3-aminopyridine following the procedure of Jones and Katritzky [8]. To obtain a colourless substance, it appears to be necessary to recrystallize twice the crude product from water in the presence of activated charcoal. The product was then recrystallized once again from water without charcoal. Finally it was dried in vacuo over P2O5. Melting point (Boetius microscope, uncorrected): 141oC (literature: 140-141oC [8]). The purity of the substance was checked by thin layer chromatography (Kieselgel-60 F254, layer thickness 0.2 mm; Merck) with the solvent systems: a) chloroform – methanol, 10:1, b) benzene – methanol, 6:1, c) benzene – dioxane, 1:1, saturated with water at 30oC. Single spots were observed (under UV light, 254 nm) with Rf-values (+0.02): a) 0.41, b) 0.44, c) 0.39 at 30oC. 1H NMR spectrum (Bruker WM-250 spectrometer, 250 MHz, (CD3)2CO solution, internal standard tetramethylsilane): 3.04 ppm, singlet, 3H – CH3; 7.36 ppm, threefold doublet (3J23=8.3 Hz, 3J34=4.7 Hz, 5J13=0.6 Hz), 1H – H(3); 7.74 ppm, threefold doublet (4J12=2.7 Hz, 4J24=1.5 Hz), 1H – H(2); 8.36 ppm, two-fold doublet, 1H – H(4); 8.54 ppm, twofold doublet, 1 H – H(1); 8.85 ppm, singlet, broad, D2O exchange – NH. The proton labeling is according to Figure 2. A partially deuterated sample of PMSA was prepared by twofold recrystallizaton of the compound from deuterium oxide (Sigma, 99.9 atom % D), followed by drying in vacuo over P2O5.
The IR spectra of PMSA and its partially deuterated analogue were recorded in the solid state as CsI (4000-150 cm-1) and KBr (4000-400 cm-1) disks, respectively, as well as in CCl4 (solution saturated at 30oC, 3.00 mm cuvette, 4000-400 cm-1) on a Bruker IFS113 spectrometer.
MM optimizations were performed with the PCMODEL 4 programme [9] which utilizes the MMX parameter set based on the Allinger MM2 force field [10]. The HF ab initio calculations were carried out with the HYPERCHEM 5 programme [11] using the 3-21G(*) basis set [12].
Results and Discussion
To find out the conformations of PMSA molecule corresponding to minima on the energy hypersurface (minimum-energy conformations, MECs), and to select among them the lowest-energy conformation (LEC) we have applied the MM method. As a result of the internal rotation about the SN and NC bonds, six enantiomeric pairs of MECs arise, and half of them are schematically depicted in Figure 1. Although the energy differences are rather small, the MECs of the EZseries (for notations see Figure 1; hereafter the signs are omitted from the MECs’ notation but it should be implied that there are enantiomeric couples which are isoenergetic) are more favorable than those of the ZE group. The LEC is of the tgG,EZ type. The MM method predicts a quasi-planar coordination around the sulfonamide nitrogen atom (the sum of its bond angles being 357o in all the MECs).
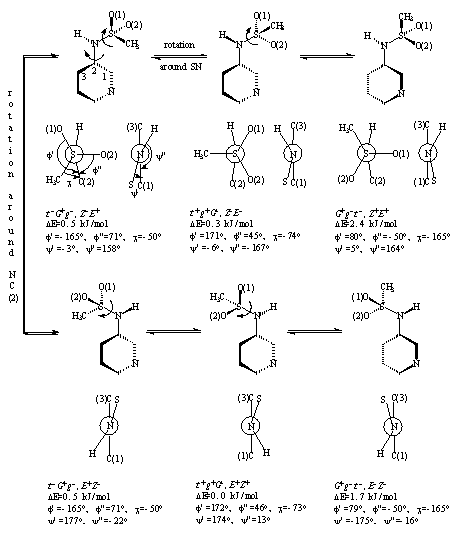
Figure 1. Molecular mechanics (MM) obtained minimum-energy conformations (MECs) of N-3-pyridinylmethanesulfonamide arising from the rotation around the SN and NC(2) bonds. The first three letters of the MEC notations refer to the torsional angles O(1)SNC(2), O(2)SNC(2) and CSNC(2), respectively: t – trans (torsional angle between 120 and 180o), G – gauche with torsional angle between 60 and 120o, g – gauche with torsional angle between 0 and 60o, with the corresponding sign. The remaining two letters refer to the torsional angles SNC(2)C(1) and HNC(2)C(1), respetively (Z – zusammen, E – entgegen). The pyridine ring is planar. The relative energies (DE) are given, the total MM energy of the lowest-energy conformation (34.5 kJ/mol) being taken as zero. There are six more MECs, each of them being a mirror image of one of the MECs depicted.
The LEC obtained by the MM method was further optimized at HF ab initiolevel and its fundamental vibrations were calculated. The 3-21G(*) basis set was chosen as a compromise between the accuracy and computational power available, but it should be noted that this basis has been found to reproduce correctly the geometry of methanesulfonamide [13]. The ab initio-optimized structure of the LEC is illustrated in Figure 2. The geometric parameters obtained by the MM and ab initio optimizations are compared in Table 1; as seen, the overall correspondence between them is good. The ab initio-calculated bond lengths and angles for the PMSA molecule are in agreement with the literature data for similar compounds [1, 13-17]. The ab initio-optimization gives a full planarization of the sulfonamide nitrogen, and this affects the torsional angles around the C(2)N(2)-bond (see Table 1). Actually, here is the main difference in the geometries predicted by the two methods.

Figure 2. A model of the ab initio optimized lowest-energy conformation of N-3-pyridinylmethanesulfonamide with the atom labelling.
| Table 1.Geometric parameters for the lowest-energy conformation of N-3-pyridinylmethanesulfonamide obtained my molecular mechanics (MM) and ab initio quantum-chemical optimization. Atom labelling is according to Figure 2. | |||||
|
Bond lengths, Å |
|||||
| Parameter | MM | ab initio | Parameter | MM | ab initio |
| N(1)C(1) | 1.365 | 1.323 | C(1)C(2) | 1.408 | 1.389 |
| C(2)C(3) | 1.408 | 1.386 | C(3)C(4) | 1.404 | 1.384 |
| C(4)C(5) | 1.403 | 1.379 | C(5)N(1) | 1.363 | 1.331 |
| C(1)H(1) | 1.103 | 1.072 | C(3)H(2) | 1.101 | 1.067 |
| C(4)H(3) | 1.103 | 1.070 | C(5)H(4) | 1.102 | 1.069 |
| C(2)N(2) | 1.373 | 1.416 | N(2)H(5) | 0.962 | 1.003 |
| N(2)S | 1.645 | 1.625 | SO(1) | 1.434 | 1.428 |
| SO(2) | 1.431 | 1.431 | SC(6) | 1.785 | 1.749 |
| C(6)H(6) | 1.113 | 1.080 | C(6)H(7) | 1.113 | 1.082 |
| C(6)H(8) | 1.113 | 1.081 | |||
|
Bond angles, deg |
|||||
| N(1)C(1)C(2) | 122 | 123 | N(1)C(1)H(1) | 118 | 117 |
| C(1)C(2)C(3) | 118 | 118 | C(1)C(2)N(2) | 116 | 118 |
| C(2)C(3)C(4) | 120 | 119 | C(2)C(3)H(2) | 122 | 120 |
| C(3)C(4)C(5) | 120 | 120 | C(3)C(4)H(3) | 120 | 120 |
| C(4)C(5)N(1) | 120 | 122 | C(4)C(5)H(4) | 121 | 121 |
| C(5)N(1)C(1) | 121 | 119 | C(2)N(2)H(5) | 116 | 118 |
| C(2)N(2)S | 126 | 128 | H(5)N(2)S | 115 | 114 |
| N(2)SO(1) | 105 | 105 | N(2)SO(2) | 110 | 110 |
| N(2)SC(6) | 109 | 103 | O(1)SC(6) | 108 | 109 |
| O(2)SC(6) | 109 | 107 | O(1)SO(2) | 116 | 120 |
| SC(6)H(6) | 110 | 110 | SC(6)H(7) | 110 | 108 |
| SC(6)H(8) | 110 | 110 | H(6)C(6)H(7) | 109 | 109 |
| H(6)C(6)H(8) | 109 | 110 | H(7)C(6)H(8) | 109 | 109 |
|
Torsional anglesa, deg |
|||||
| C(1)C(2)N(2)H(5) | 13 | -23 | C(1)C(2)N(2)S | 174 | 161 |
| C(3)C(2)N(2)H(5) | -168 | 156 | C(3)C(2)N(2)S | -6 | -20 |
| C(2)N(2)SO(1) | 172 | 172 | C(2)N(2)SO(2) | 46 | 41 |
| C(2)N(2)SC(6) | -73 | -73 | H(5)N(2)SO(1) | -28 | -4 |
| H(5)N(2)SO(2) | -153 | -135 | H(5)N(2)SC(6) | 88 | 111 |
| N(2)SC(6)H(6) | -55 | -65 | N(2)SC(6)H(7) | -175 | 175 |
| N(2)SC(6)H(8) | 65 | 56 | O(1)SC(6)H(6) | 59 | 47 |
| O(1)SC(6)H(7) | -61 | -73 | O(1)SC(6)H(8) | 179 | 168 |
| O(2)SC(6)H(6) | -175 | 179 | O(2)SC(6)H(7) | 65 | 59 |
| O(2)SC(6)H(8) | -55 | -60 | |||
| a The pyridine ring is planar. | |||||
The solid-state IR spectrum of PMSA is presented in Figure 3 and the assignments of the fundamental vibrations are presented in Table 2. In Figure 4 the IR spectra of the deuterated compound in solid state and in CCl4 solution are shown. The assignments proposed are based on the literature data for molecules containing related structural fragments, namely: pyridine and substituted pyridines [17, 18-26], including amimopyridines [27-29]; methanesulfonyl derivatives [1-3, 30-34], including methanesulfonamide [35] and N-arylmethanesulfonamides [36-38]. For the notations of the vibrational modes of the pyridine fragment of PMSA, we have accepted the scheme based on the correlation between the pyridine and benzene modes according to Wilson [24]. The fundamental vibrational modes of the ab initio-optimized conformation of PMSA (Figure 2) were calculated with the same basis set; the results are included in Table 2. The assignment of the calculated wave numbers was aided by the animation option of the HYPERCHEM programme which gives a visual presentation of the shape of the vibrational modes. We checked the reliability of the ab inito-vibrational analysis with the 3-21G(*) basis set on the examples of 3-aminopyridine and methanesulfonamide. The scaling factors for the wave numbers (n~exptl/n~calcd) were in the range of 0.82-1.02. As seen from Table 2, the scaling factors for PMSA fall typically in the range of 0.84-0.93, but there are some deviations. For example, the wave numbers of the modes py(5), py(17a) and py(10b) (for notations, see Table 2) are considerably overestimated, the scaling factors being 0.81-0.82; on the other hand, for the lowest frequency modes the scaling factors are about 1. Similar features were found from our control calculations on 3-aminopyridine.
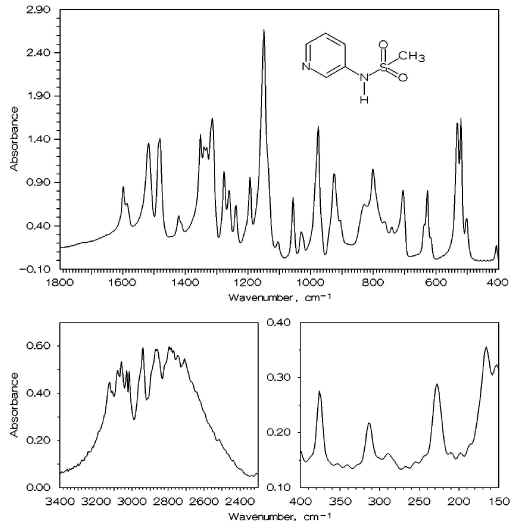
Figure 3. IR spectrum of N-3-pyridinylmethanesulfonamide in CsI disk.
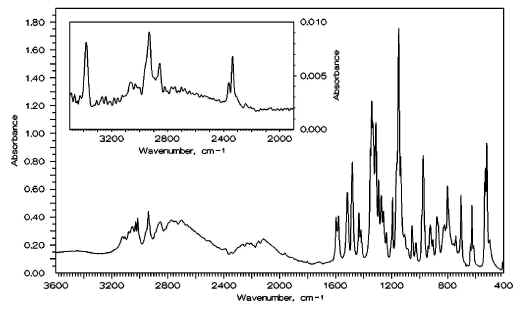
Figure 4. IR spectra of partially deuterated N-3-pyridinylmethanesulfonamide: in KBr disk (the large figure) and in saturated solution in CCl4 (the small figure).
|
Table 2. Experimental (solid-state IR spectrum) and calculated (ab initio) wave numbers (n~, cm-1) of the fundamental vibrations of N-3-pyridinylmethanesulfonamide. |
||||
| No | n~exptl | n~calcd(relative intensity) |
n~exptl/n~calcd |
Approximate assignmentb |
|
1 |
3383 ma – CC4soln. 2860-2709 m, b, c – solid |
3758 (0.320) |
0.900 |
n(NH)c |
|
2 |
3124 w |
3435 (0.023) |
0.909 |
n(CH)py – py(2) |
|
3 |
3108 w |
3403 (0.050) |
0.913 |
n(CH)py – py(20b) |
|
4 |
3080 m |
3382 (0.017) |
0.911 |
n(CH)py – py(7b) |
|
5 |
3059 m |
3363 (0.066) |
0.910 |
n(CH)py – py(20a) |
|
6 |
3030 m |
3319 (0.001) |
0.913 |
nas(CH3) |
|
7 |
3016 m |
3304 (0.001) |
0.913 |
nas(CH3) |
|
8 |
2939 m |
3225 (0.001) |
0.911 |
ns(CH3) |
|
9 |
1598 m |
1755 (0.090) |
0.911 |
n(ring) – py(8a) |
|
10 |
1585 m |
1739 (0.006) |
0.911 |
n(ring) -py(8b) |
|
11 |
1518 s |
1650 (0.026) |
0.920 |
n(ring)+d(CH)py – py(19a), n(NH) |
|
12 |
1481 s |
1625 (0.832) |
0.911 |
n(ring)+d(CH)py – py(19b) |
|
13 |
1421 m |
1628 (0.094) |
0.873 |
das(CH3) |
|
14 |
1410 sh |
1622 (0.025) |
0.869 |
das(CH3) |
|
15 |
Masked by No 14 or No 16 |
1554 (0.374) |
0.907 or 0.869 |
d(NH), n(ring)+nas(SO2) |
|
16 |
1351 s, 1341 s |
1460 (0.347) |
0.913 (ave.) |
nas(SO2), d(NH) +n(ring) |
|
17 |
1330 s |
1573 (0.125) |
0.846 |
ds(CH3) |
|
18 |
1314 s |
1523 (0.256) |
0.863 |
n(ring)+d(CH)py – py(14), nas(SO2) |
|
19 |
1276 m, 1260 m |
1355 (0.177) |
0.936 (ave.) |
n(CN) – py(13) |
|
20 |
1238 m |
1358 (0.153) |
0.912 |
n(ring)+d(CH)py – py(9a) |
|
21 |
1193 m |
1251 (0.100) |
0.954 |
n(ring)+d(CH)py – py(3) |
|
22 |
1150 s |
1276 (1.000) |
0.901 |
ns(SO2) |
|
23 |
1105 w |
1192 (0.015) |
0.927 |
n(ring)+d(CH)py – py(18b) |
|
24 |
1056 m |
1135 (0.097) |
0.930 |
n(ring)+d(CH)py – py(18a) |
|
25 |
1030 w |
1160 (0.074) |
0.888 |
n(ring) – py(1) |
|
26 |
985 sh |
1223 (0.046) |
0.805 |
p(CH) – py(5) |
|
27 |
976 s |
1127 (0.248) |
0.866 |
r(CH3) |
|
28 |
960 sh |
1120 (0.009) |
0.857 |
r(CH3) |
|
29 |
940 sh |
1150 (0.019) |
0.817 |
p(CH) – py(17a) |
|
30 |
925 m |
1042 (0.618) |
0.888 |
n(SN) |
|
31 |
905 w |
1114 (0.026) |
0.812 |
p(CH) – py(10b) |
|
32 |
829 m |
975 (0.187) |
0.850 |
p(CH) – py(10a) |
|
33 |
801 m |
908 (0.148) |
0.882 |
d(ring) – py(12) |
|
34 |
762 m |
845 (0.305) |
0.902 |
n(CS) |
|
35 |
705 m |
836 (0.016) |
0.843 |
t(ring)+p(CN) – py(4) |
|
36 |
638 sh |
736 (0.012) |
0.867 |
d(ring) – py(6b) |
|
37 |
627 m |
643 (0.235) |
0.975 |
p(NH) |
|
38 |
612 sh |
697 (0.085) |
0.878 |
d(ring) – py(6a) |
|
39 |
531 s |
591 (0.256) |
0.898 |
d(SO2) |
|
40 |
520 s |
580 (0.254) |
0.897 |
w(SO2) |
|
41 |
500 m |
497 (0.089) |
1.006 |
t(ring)+p(CN) – py(11) |
|
42 |
490 sh |
484 (0.069) |
1.012 |
t(ring) – py(16a) |
|
43 |
407 w |
399 (0.008) |
1.020 |
r(SO2) |
|
44 |
376 w |
374 (0.035) |
1.005 |
d(CSN) |
|
45 |
313 w |
335 (0.012) |
0.934 |
d(CN) – py(15) |
|
46 |
289 w |
314 (0.006) |
0.920 |
t(SO2) |
|
47 |
244 w |
243 (0.005) |
1.004 |
t(ring) – py(16b) |
|
48 |
228 w |
238 (0.012) |
0.958 |
t(CS) |
|
49 |
166 w |
170 (0.025) |
0.976 |
d(CNS) |
|
50 |
67 (0.025) |
t(SN) |
||
|
51 |
46 (0.019) |
t(CN) |
||
|
a Abbreviations: b – broad, c – complex, m – medium, s – strong, sh – shoulder, w – weak. |
||||
Some bands in the IR spectrum (nas(SO2), n(CN)) are split, which could be attributed to solid-state effects. The unassigned band at 153 cm-1 might tentatively be ascribed to a lattice mode. The two lowest-frequency modes (t(SN) and t(CN)) that are expected below 150 cm-1 [1, 3] were not observed because of instrumental restrictions.
Special attention should be paid to the NH-vibrations. In the solid-state spectrum (see Figure 3), there are no bands above 3200 cm-1 but a broad band split into several components is seen in the interval 2900-2500 cm-1. This band disappears from the spectrum of PMSA taken in CCl4 solution, and a single one appears at 3383 cm-1. We have assigned these latter bands to the NH stretching vibration. This assignment was confirmed by deuteration: in the solid-state spectrum of the deuterated sample, a new complex band appears in the range of 2180-2000 cm-1, and in the CCl4 solution spectrum – a single band is found at 2337 cm-1 (see Figure 4). The pronounced decrease in the NH stretching frequency in solid state is remarkable and it must be explained by the presence of strong intermolecular hydrogen bonds between the pyridine nitrogen and the hydrogen of the NH group which is known to be rather acidic in sulfonamides [13]. The formation of intermolecular hydrogen bonds between the basic amino nitrogen atom and the acidic hydrogen of the sufonamide group has been recorded by as and reported in ref [1] in crystalline methanesulfonylhydrazine, although the lowering of the n(NH) frequency in this case was not so significant. The position and the shape of the NH-stretching band in the solid-state spectrum of PMSA is similar to that of the OH-stretching of a number of salicylaldehyde Schiff bases [2, 39-42] characterized by the presence of a very strong hydrogen bond between the hydroxyl group and the imine nitrogen atom.
The band corresponding to the NH in-plane bending vibration of PMSA is expected near 1400 cm-1 [1-3, 38]. We were not able to distinguish this band probably because it is masked by the band of das(CH3) at 1410 cm-1 or the band of nas(SO2) at 1351 cm-1. In the spectrum of the deuterated PMSA, however, two new bands appear at 1434 and 1293 cm-1. The second one should be attributed to the ND bending vibration. The isotopic ratio, n~H/n~D, appears relatively small, 1.09-1.04, but this is explainable taking into account that the ab initio calculations show that the d(NH)-vibration is not pure and contains a significant contribution of other modes (n(ring) and nas(SO2)). On the other hand, the new band at 1434 cm-1 in the spectrum of the deuterated sample could be ascribed to vibration No 11, affected by the isotopic exchange (n~H/n~D=1.06). This suggestion is supported by the ab initio results showing that the corresponding fundamental is not pure py(19a)-vibration and contains a considerable contribution from the d(NH) motion. In accordance with literature data [1-3, 38], we have assigned the band at 627 cm-1 to the out-of-pane bending mode of the NH-group (p(NH)), but we did not succeed in identifying the corresponding band of the deuterated compound. It probably falls in the range of 530-500 cm-1, and is obscured by the SO2-deformation modes.
Conclusion
The molecular mechanics method was applied for conformational modelling of N-3-pyridinylmethanesulfonamide, a pharmacologically interesting compound. The lowest-energy conformation thus obtained was further optimized at the HF ab initio level with the 3-21G(*) basis set and vibrational analysis was performed by the same method. The geometries calculated by the two approaches are similar.
The IR spectrum of the compound in the solid state was studied in the interval of 4000-150 cm-1, as well as in CCl4 solution in the high-frequency region. An assignment of the IR bands was proposed on the basis of literature data for similar compounds and of an ab intio vibrational analysis. The assignment of the vibrations of the NH-group was confirmed by deuteration. The solid-state IR spectrum reveals for the NH stretching vibration a broad band in the range of 2900-2500 cm-1, whereas in solution it appears at 3383 cm-1. The significant low-frequency shift of the NH stretching band in the solid state as compared with the solution is explained by the existence in the solid state of a strong intermolecular hydrogen bond between the pyridine nitrogen atom and the acidic hydrogen of the sulfonamide group. It must be assumed that polymeric chains exist, consisting in PMSA molecules connected between each other via the pyridine nitrogen and the hydrogen of the sulfonamide group. It should be interesting to check this supposition by single crystal X-ray diffraction analysis.
Acknowledgement
The author thanks the UNESCO Global Network for Molecular and Cell Biology (MCBN) for the financial support (Grant No 436).
References
- A. Ienco, C. Mealli, P. Paoli, N. Dodoff, Z. Kantarci, N. Karacan, New J. Chem., 23, 1253 (1999).
- N. I. Dodoff, Ü. Özdemir, N. Karacan, M. Ch. Georgieva, S. M. Konstantinov, M. E. Stefanova, Z. Naturforsch., B, 54, 1553 (1999).
- N. I. Dodoff, Internet J. Vibr. Spectrosc., 3, 4, 7 (1999) [www.irdg.org/ijvs.
- N. R. Lomax, V. L. Narayanan, “Chemical Structures of Interest to the Division of Cancer Treatment”, Vol. VI, Developmental Therapeutics Program, National Cancer Institute, Bethesda, MD, 1988.
- P. B. Jensen, B. S. Soerensen, J. F. E. Demant, M. Sehested, P. S. Jensen, L. Vindeloey, H. H. Hansen, Cancer Res., 50, 3311 (1990).
- G. J. Finlay, B. C. Baguley, K. Snow, W. Judd, J. Natl. Cancer Inst., 82, 662 (1990).
- D. D. Perrin, W. F. F. Armarego, D. R. Perrin, “Purification of Laboratory Chemicals”, Pergamon Press, Oxford, 1980.
- R. A. Jones, A. R. Katritzky, J. Chem. Soc., 1961, 378.
- PCMODEL, Molecular Modelling Software, Serena Software, Bloomington, IN, 1990.
- N. L. Allinger, J. Am. Chem. Soc., 99, 8127 (1977).
- HYPERCHEM 5, Molecular Modelling System, Hypercube, Inc., Gainesville, FL, 1997.
- W. J. Pietro, M. M. Francl, W. J. Hehre, D. J. DeFrees, J. A. Pople, J. S. Binkley, J. Am. Chem. Soc., 104, 5039 (1982).
- S. Topiol, M. Sabio, P. W. Erhardt, J. Chem Soc., Perkin Trans. 2, 1988, 437.
- A. N. Chekhlov, I. V. Martynov, Kristallografiya, 33, 1527 (1988).
- Yu. A. Simonov, A. A. Dvorkin, M. D. Mazus, I. A. Popa, V. N. Shafranskiy, ibid., 35, 1145 (1990).
- P. Lightfoot, M. Tremayne, C. Glidewell, K. D. M. Harris, P. G. Bruce, J. Chem. Soc., Perkin Trans. 2, 1993, 1625.
- E. Cebe, M. Cebe, S. Erdem, Chim. Acta Turcica, 25, 43 (1997).
- E. Wachsmann, E. W. Schmid, Z. Physik. Chem., Neue Folge, 27, 145 (1961).
- a) D. A. Long, F. S. Murfin, E. L. Thomas, Trans. Faraday Soc., 59, 12 (1963); b) D. A. Long, E. L. Thomas, ibid., 59, 783 (1963).
- J. H. S. Green, W. Kynaston, H. M. Paisley, Spectrochim. Acta, 19, 549 (1963).
- J. R. Durig, B. R. Mitchel, D. W. Sink, J. N. Willis, Jr., A. S. Wilson, ibid., 23A, 1121 (1967).
- V. I. Breezin, M. D. El’kin, Optika i Spektroskopiya, 34, 685 (1973).
- a) H. D. Stidham, D. P. DiLella, J. Raman Spectrosc., 8, 180 (1979); b) D. P. DiLella, H. D. Stidham, ibid., 9, 90 (1980); c) D. P. DiLella, ibid., 9, 239 (1980); d) H. D. Stidham, D. P. DiLella, ibid., 9, 247 (1980).
- J. A. Draeger, Spectrochim. Acta, 39A, 809 (1983).
- a) K. B. Wiberg, V. A. Walters, K. N. Wong, S. D. Colson, J. Phys. Chem., 88, 6067 (1984); b) K. N. Wong, S. D. Colson, J. Molec. Spectrosc., 104, 129 (1984).
- G. Pongor, P. Pulay, G. Fogarasi, J. E. Boggs, J. Am. Chem. Soc., 106, 2765 (1984).
- J. Baran, Z. Malarski, L. Sobczyk, E. Grech, Spectrochim. Acta, 44A, 933 (1988).
- P. Carmona, M. Molina, ibid., 49A, 1 (1993).
- a) S. Mohan, V. Ilangovan, Procs. Natl. Acad. Sci. India, 65A, 357 (1995); b) S. Mohan, K. Settu, ibid., 65A, 105 (1995).
- R. J. W. Cremlyn, D. N. Waters, J. Chem. Soc., Suppl. 2, 1964, 6243.
- R. D. McLachlan, V. B. Carter, Spectrochim. Acta, 26A, 1121 (1970).
- a) T. Uno, K. Machida, K. Hanai, ibid., 27A, 107 (1971); b) K. Hanai, T. Okuda, K. Machida, ibid., 31A, 1227 (1975).
- G. Geiseler, G. Hanschmann, J. Molec. Struct., 8, 293 (1971).
- G. Chassaing, J. Corset, J. Limouzi, Spectrochim. Acta, 37A, 721 (1981).
- K. Hanai, T. Okuda, T. Uno, K. Machida, ibid., 31A, 1217 (1975).
- A. R. Katritzky, R. A. Jones, J. Chem. Soc., 1960, 4497.
- Yu. Tanaka, Yo. Tanaka, Chem.-Pharm. Bull., 13, 858 (1965).
- K. Hanai, A. Noguchi, T. Okuda, Spectrochim. Acta, 34A, 771 (1978).
- P. Teyssie, J. J. Charette, ibid, 19, 1407 (1963).
- G. C. Percy, D. A. Thornton, J. Inorg. Nucl. Chem., 34, 3357 (1972).
- J. A. Faniran, K. S. Patel, J. S. Bailar, Jr., ibid., 36, 1574 (1974).
- M. Carles, D. Eloy, L. Pujol, H. Bodot, J. Molec. Struct., 156, 43 (1987).
REF: N. I. Dodoff, Int. J. Vib. Spect., [www.irdg.org/ijvs] 4, 3, 5 (2000)

