Normal Coordinate Analysis of Acetone Methanesulfonylhydrazone
CONTRIBUTED ARTICLE
7. Normal Coordinate Analysis of Acetone Methanesulfonylhydrazone
Nicolay I. Dodoff
Institute of Molecular Biology,
Bulgarian Academy of Sciences,
Acad. G. Bonchev Street,
Block 21, 1113 Sofia,
Bulgaria.
dodoff [at] bas.bg (E-mail:)dodoff [at] bas.bg ( )
Abstract
An assignment of the solid-state IR spectrum of acetone methanesulfonylhydrazone in the range of 4000-150 cm-1 has been proposed on the basis of a normal coordinate analysis of a single molecule. The harmonic general valence force field has been applied. The geometry of the lowest-energy conformation as found by molecular mechanics method has been used.
Key words
Acetone methanesulfonylhydrazone, IR spectra, Normal coordinate analysis, Molecular mechanics.
Introduction
Methanesulfonamide derivatives [1-4], as well as compounds containing hydrazine or hydrazone residue [5] are of interest in pharmacology, and especially, in cancer chemotherapy. Recently [6] we have prepared and studied a series of azomethine derivatives of methanesulfonylhydrazine which exhibit antibacterial and cytostatic activity. Acetone methanesulfonylhydrazone, (CH3)2C=NNHS(O)2CH3 (AMSH) has been described in the literature [7] but has not been characterized spectroscopically. In [6] we proposed a qualitative interpretation of the spectrum of AMSH in the mid IR region. Here we present a more reliable assignment of the mid and far IR bands of this compound, based on normal coordinate analysis (NCA).
Experimental
Methanesulfonylhydrazine was prepared according to [7]. The remaining chemicals were commercial products.
AMSH was prepared from acetone and methanesulfonylhydrazine as described in [7]. M. p. 120oC (Boetius microscope; uncorrected). TLC (silica gel on glass; benzene-acetone-methanol, 5:5:2): Rf=0.90± 0.03. 1H NMR (Bruker WM-400 spectrometer, 400 MHz; DMSO-d6 solution; internal standard TMS): 1.82, s, 3H, 1.92, s, 3H ((CH3)2C=N); 2.95, s, 3H (CH3S); 9.40, s, 1H (NH).
The IR spectrum of AMSH was recorded as a CsI disk on a Bruker IFS113 spectrometer in the range of 4000-150 cm-1.
Molecular mechanical calculations were carried out with the PCMODEL 4 programme [8] which utilizes the MMX parameter set based on the Allinger MM2 force field [9].
The normal coordinate analysis of a single AMSH molecule within a harmonic generalized valence force field was reformed by the MOLVIB 6 programme of T. Sundius [10-12].
Results and Discussion
In [6] we studied the conformational isomerism of AMSH and other azomethine derivatives of methanesulfonylhydrazine by means of the molecular mechanical method. In Figure 1 the structure of the lowest-energy conformation of AMSH is depicted (there is another isoenergetic structure which is a mirror image of that shown), and its geometric parameters are collected in Table 1. The kinematic coefficient G matrix was calculated from this geometry.
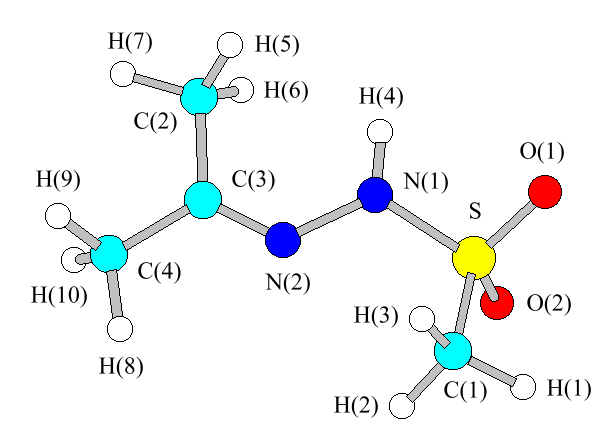
Figure 1. Molecular mechanics derived lowest-energy conformation of AMSH with the atom labelling scheme.
|
Bond lengths, Å |
||||||||
| H(1)C(1) | 1.113 | H(2)C(1) | 1.113 | H(3)C(1) | 1.113 | C(1)S | 1.782 | |
| SO(1) | 1.433 | SO(2) | 1.433 | SN(1) | 1.642 | H(4)N(1) | 0.959 | |
| N(1)N(2) | 1.423 | N(2)C(3) | 1.275 | C(2)C(3) | 1.506 | C(4)C(3) | 1.505 | |
| H(5)C(2) | 1.114 | H(6)C(2) | 1.114 | H(7)C(2) | 1.113 | H(8)C(4) | 1.114 | |
| H(9)C(4) | 1.114 | H(10)C(4) | 1.114 | |||||
|
Bond angles, deg |
||||||||
| H(1)C(1)H(2) | 109 | H(1)C(1)H(3) | 109 | |||||
| H(2)C(1)H(3) | 109 | H(1)C(1)S | 110 | |||||
| H(2)C(1)S | 110 | H(3)C(1)S | 110 | |||||
| C(1)SN(1) | 110 | C(1)SO(1) | 108 | |||||
| C(1)SO(2) | 108 | O(1)SO(2) | 117 | |||||
| O(1)SN(1) | 106 | O(2)SN(1) | 107 | |||||
| SN(1)H(4) | 118 | SN(1)N(2) | 120 | |||||
| H(4)N(1)N(2) | 120 | N(1)N(2)C(3) | 124 | |||||
| N(2)C(3)C(2) | 123 | N(2)C(3)C(4) | 120 | |||||
| C(2)C(3)C(4) | 118 | H(5)C(2)C(3) | 111 | |||||
| H(6)C(2)C(3) | 110 | H(7)C(2)C(3) | 112 | |||||
| H(5)C(2)H(6) | 109 | H(5)C(2)H(7) | 108 | |||||
| H(6)C(2)H(7) | 108 | H(8)C(4)C(3) | 112 | |||||
| H(9)C(4)C(3) | 110 | H(10)C(4)C(3) | 110 | |||||
| H(8)C(4)H(9) | 108 | H(8)C(4)H(10) | 108 | |||||
| H(9)C(4)H(10) | 109 | |||||||
|
Torsional angles, deg |
||||||||
| H(1)C(1)SN(1) | -172 | H(1)C(1)SO(1) | -57 | |||||
| H(1)C(1)SO(2) | 71 | H(2)C(1)SN(1) | 68 | |||||
| H(2)C(1)SO(1) | -176 | H(2)C(1)SO(2) | -49 | |||||
| H(3)C(1)SN(1) | -52 | H(3)C(1)SO(1) | 63 | |||||
| H(3)C(1)SO(2) | -169 | C(1)SN(1)H(4) | 162 | |||||
| C(1)SN(1)N(2) | -35 | O(1)SN(1)H(4) | 44 | |||||
| O(1)SN(1)N(2) | -152 | O(2)SN(1)H(4) | -81 | |||||
| O(2)SN(1)N(2) | 83 | H(4)N(1)N(2)C(3) | -7 | |||||
| SN(1)N(2)C(3) | -171 | N(1)N(2)C(3)C(2) | 0 | |||||
| N(1)N(2)C(3)C(4) | 180 | H(5)C(2)C(3)C(4) | 122 | |||||
| H(5)C(2)C(3)N(2) | -58 | H(6)C(2)C(3)C(4) | -117 | |||||
| H(6)C(2)C(3)N(2) | 62 | H(7)C(2)C(3)C(4) | 2 | |||||
| H(7)C(2)C(3)N(2) | -178 | H(8)C(4)C(3)C(2) | -179 | |||||
| H(8)C(4)C(3)N(2) | 1 | H(9)C(4)C(3)C(2) | -60 | |||||
| H(9)C(4)C(3)N(2) | 121 | H(10)C(4)C(3)C(2) | 60 | |||||
| H(10)C(4)C(3)N(2) | -119 | |||||||
Table 1.Geometric parameters for the lowest-energy conformation of AMSH. Atom labeling is according to Figure 1.
The assignment of the IR bands of AMSH was made taking into consideration the data available for other compounds containing appropriate structural fragments: vis. methanesulfonylhydrazine [13], the methanesulfonamides [14-17] and other methanesulfonyl derivatives [18-22]; acetone [23] and compounds containing the (CH3)2C=X (X = N, O, C) residue [24-26].
The experimental wave numbers and the NCA results are collected together in Table 2, and the optimized force field is defined in Table 3. To overcome the deficiency in the experimental wave numbers with respect to the number of F matrix elements, the values of some force constants were not varied during the optimization procedure. As seen from Table 2, the agreement between the experimental and calculated wave numbers is good, the RMS error being 1.3%. The largest deviation (150 vs. 137 cm-1) concerns the d(SNN) mode, but this band should fall below 150 cm-1, i.e. outside the range of our spectrometer. Because of instrumental restrictions, the lowest-frequency vibrations, corresponding to t(SN) and t(NN) were not observed. The calculated wave numbers of these modes were obtained by giving the force constants for the torsions around the SN and NN bonds a value similar to that of the force constant of the SN torsion from the normal coordinate analysis (NCA) of methanesulfonylhydrazine [13]. The classification of the vibrational modes into types like νas, νs, ω, ρ etc. was confirmed by checking the signs of the corresponding L matrix elements. As seen from the potential energy distribution (PED) (Table 2), some of the vibrational modes are quite mixed, and they could only very approximately be regarded as localized vibrations.
The direct comparison between the AMSH force constants obtained and the literature data for some related molecules [16, 19-22] is not justified, because of the differently defined force fields used by other authors. The force constants for the CH3S(O)2NHN fragment of AMSH are, however, in agreement with that found by us from the normal coordinate analysis of methanesulfonylhydrazine [13].
The splitting observed for some IR bands (Table II) should be attributed to solid state effects. We could not comment on this feature in detail, because of the lack of crystal structure data for AMSH. It should be mentioned, however, that in all cases, except the doublet at 1654 and 1640 cm-1, the splitting concerns bands corresponding to vibrations involving the NH and SO2 groups, thus implying the presence of hydrogen bonding in the solid state.
| Experimental | Calcd. | Relative error, % | PED, %a | Assignment |
| – | 49 | – | 46 t(SN), 31 t(NN), 15 t(NC) | t(SN)b |
| – | 71 | – | 38 t(NN), 24 t(SN), 19 p(N), 11p(C) | t(NN) |
| 150wc | 137 | 8.67 | 38 SNN, 38 CNN | δ(SNN) |
| 170w | 171 | -0.59 | 96 t(CS) | t(CS) |
| 201w | 201 | 0.00 | 89 t(CC) | t(CC) |
| 209w | 207 | 0.96 | 99 t(CC) | t(CC) |
| 225w | 227 | -0.89 | 25 NNC, 19 SN, 10 SNN | δ(NNC) |
| 243w | 246 | -1.23 | 65 π(C) | π(CC2) |
| 320m | 318 | 0.63 | 33 NSO, 30 CSN, 10 NN | δ(CSN) |
| 370m | 364 | 1.62 | 26 t(NC), 20 p(C), 20 CSO, 16 NSO | t(NC) |
| 382m | 388 | -1.57 | 43 CSO, 27 t(NC), 10 NSO | t(SO2) |
| 412w | 415 | -0.73 | 31 CSO, 24 NSO, 13 CSN | τ(SO2) |
| 450w457d
464sh |
453 | 0.88 | 31 CSO, 29 NSO, 11 CCC | ω(SO2) |
| 492m | 492 | 0.00 | 28 OSO, 25 CCC, 13 NCC, 13 CSO | δ(CC2) |
| 517sh521d
525m |
521 | 0.00 | 35 OSO, 12 SNN, 11 CCC, 10 NCC | δ(SO2) |
| 567m | 566 | 0.18 | 35 NCC, 19 CC, 14 NSO, 10 NNC | δ(NCC) |
| 652m | 654 | -0.3 | 48 p(N), 14 t(NN), 11 NSO | ρ(NH) |
| 770m | 770 | 0.00 | 40 CS, 18 SN, 10 CC | ν(CS) |
| 819m | 819 | 0.00 | 47 CC, 16 SN, 11 NC | ns(CC2) |
| 914m | 914 | 0.00 | 33 SN, 16 HCS, 10 CC, 10 CS | ν(SN) |
| 974s | 972 | 0.21 | 41 HCC’, 33 CC | ρ(CH3)C |
| – | 973 | – | 81 HCS | ρ(CH3)S |
| 990sh | 990 | 0.00 | 68 HCS | ρ(CH3)S |
| – | 1012 | – | 47 HCC”, 43 HCC’ | ρ(CH3)C |
| 1018w | 1018 | 0.00 | 57 HCC” | ρ(CH3)C |
| 1078sh | 1078 | 0.00 | 45 HCC’, 40 HCC” | ρ(CH3)C |
| 1094m | 1094 | 0.00 | 38 NN, 22 HCC’, 12 CC | ν(NN) |
| 1152s1162d
1172s |
1162 | 0.00 | 78 SO | νs(SO2) |
| 1273m | 1273 | 0.00 | 31 CC, 19 NCC, 12 HCC”, 11 HCC’ | νas(CC2) |
| 1320sh | 1320 | 0.00 | 49 HCS, 32 HCH, 14 CS | δs(CH3)S |
| 1330s | 1330 | 0.00 | 89 SO | νas(SO2) |
| 1369m | 1368 | 0.07 | 27 HCC’, 26 HCC”, 21 HCH’, 20 HCH” | δs(CH3)C |
| 1397sh | 1396 | 0.07 | 29 HNN, 28 HNS | δ(NH) |
| 1403m | 1404 | -0.07 | 16 HCH”, 14 HCC’, 13 HCH’, 11 HCC” | δs(CH3)C |
| – | 1424 | – | 85 HCH, 11 HCS | δas(CH3)S |
| 1425m | 1425 | 0.00 | 83 HCH, 11 HCS | δas(CH3)S |
| – | 1429 | – | 50 HCH”, 37 HCH’ | δas(CH3)C |
| – | 1432 | – | 47 HCH’, 32 HCH” | δas(CH3)C |
| 1434sh | 1434 | 0.00 | 65 HCH’, 23 HCH” | δas(CH3)C |
| 1440sh | 1440 | 0.00 | 64 HCH”, 21 HCH’ | δas(CH3)C |
| 1654m1647d
1640sh |
1652 | -0.30 | 57 NC, 12 CC | ν(NC) |
| 2925w | 2925 | 0.00 | 64 CH”, 35 CH’ | νs(CH3)C |
| – | 2926 | – | 65 CH’, 35 CH” | νs(CH3)C |
| 2934w | 2934 | 0.00 | 100 CH | νs(CH3)S |
| – | 2996 | – | 70 CH’, 29 CH” | νas(CH3)C |
| – | 2997 | – | 99 CH” | νas(CH3)C |
| – | 2998 | – | 100 CH’ | νas(CH3)C |
| 2999m | 2999 | 0.00 | 70 CH”, 29 CH’ | νas(CH3)C |
| – | 3019 | – | 100 CH | νas(CH3)S |
| 3019w | 3019 | 0.00 | 100 CH | νas(CH3)S |
| 3154m3185d
3215m |
3185 | 0.00 | 100 NH | ν(NH) |
Table 2. Experimental and calculated wave numbers (cm-1) of the fundamental vibrations of AMSH
aPotential energy distribution; the components less than 10% are omitted.
bNotations: as – antisymmetric, s – symmetric, t – torsional, δ – bending, ν – stretching, π – out-of-plane bending, ρ– rocking, τ– twisting, ω – wagging.
cAbbreviations: m – medium, s – strong, sh – shoulder, w – weak.
dThe averaged of the pair of wave numbers.
| Internal coodinatea | Force constantb | |
| Notation | Definition | |
| Stretching | ||
| CH | C(1)H(1), C(1)H(2), C(1)H(3) | 4.883c |
| CS | C(1)S | 4.212 |
| SN | SN(1) | 4.212 |
| SO | SO(1), SO(2) | 9.196c |
| NH | N(1)H(4) | 5.600c |
| NN | N(1)N(2) | 4.547 |
| NC | N(2)C(3) | 6.911 |
| CC’ | C(2)C(3) | 4.366 |
| CC” | C(4)C(3) | 4.366 |
| CH’ | C(2)H(5), C(2)H(6), C(2)H(7) | 4.867c |
| CH” | C(4)H(8), C(4)H(9), C(4)H(10) | 4.867c |
| In-plane bending | ||
| HCH | H(1)C(1)H(2), H(1)C(1)H(3), H(2)C(1)H(3) | 0.429 |
| HCS | H(1)C(1)S, H(2)C(1)S, H(3)C91)S | 0.693 |
| CSO | C(1)SO(1), C(1)SO(2) | 1.415 |
| NSO | N(1)SO(1), N(1)SO(2) | 1.415 |
| OSO | O(1)SO(2) | 1.468 |
| CSN | C(1)SN(1) | 1.179 |
| SNN | SN(1)N(2) | 1.196 |
| HNS | H(4)N(1)S | 0.492 |
| HNN | H(4)N(1)N(2) | 0.492 |
| NNC | N(1)N(2)C(3) | 1.260 |
| NCC’ | N(2)C(3)C(2) | 1.564 |
| NCC” | N(2)C(3)C(4) | 1.564 |
| CCC | C(2)C(3)C(4) | 1.476 |
| HCC’ | H(5)C(2)C(3), H(6)C(2)C(3), H(7)C(2)C(3) | 0.733 |
| HCC” | H(8)C(4)C(3), H(9)C(4)C(3), H(10)C(4)C(3) | 0.733 |
| HCH’ | H(5)C(2)H(6), H(5)C(2)H(7), H(6)C(2)H(7) | 0.518 |
| HCH” | H(8)C(4)H(9), H(8)C(4)H(10), H(9)C(4)H(10) | 0.518 |
| Out-of-plane bending | ||
| p(N) | at N(1) | 0.081c |
| p(C) | at C(2) | 0.105c |
| Torsional | ||
| t(CS) | around C(1)S | 0.055c |
| t(SN) | around SN(1) | 0.098c |
| t(NN) | around N(1)N(2) | 0.098c |
| t(NC) | around N(2)C(3) | 0.400c |
| t(CC) | around C(2)C(3), around C(4)C(3) | 0.080c |
| Off-diagonal | ||
| CH-CH | 0.031 | |
| CS-SN | 0.296 | |
| SO-SO | 0.056 | |
| SN-NN | 0.119 | |
| CC’-CC” | 0.588 | |
| CH’-CH’ | 0.038 | |
| CH”-CH” | 0.038 | |
| NN-HNN | 0.055 | |
| CC’-NCC’ | 0.317 | |
| CC”-NCC” | 0.317 | |
| CC’-HCC’ | 0.405 | |
| CC”-HCC” | 0.405 | |
| HC’-HCC’ | 0.049 | |
| HC”-HCC” | 0.049 | |
| HC’-HCH’ | 0.160 | |
| HC”-HCH” | 0.160 | |
| HCH-HCH | -0.106 | |
| HCS-HCS | 0.013 | |
| CSO-CSO | 0.170 | |
| CSO-NSO | 0.170 | |
| NSO-NSO | 0.170 | |
| CSO-CSN | -0.157 | |
| NSO-CSN | -0.157 | |
| CSN-SNN | 0.345 | |
| HNS-HNN | 0.054 | |
| NNC-NCC’ | 0.275 | |
| NNC-NCC” | -0.077 | |
| CCC-NCC’ | 0.089 | |
| CCC-NCC” | 0.089 | |
| HCH’-HCH’ | -0.026 | |
| HCH”-HCH” | -0.026 | |
| p(N)-t(NN) | 0.020c | |
| p(C)-t(NC) | -0.071c | |
Table 3. Internal coordinates and optimized force constants for AMSH.
Table 3. Internal coordinates and optimized force constants for AMSH.
aAtom numbering according to Figure 1.
bUnits: mdyn·Å-1 – stretching and off-diagonal stretching-stretching; mdyn·Å·rad-2 – bending and off-diagonal bending-bending; mdin·rad-1 – off-diagonal stretching-bending.
cKept constant during optimization.
Conclusion
As can be seen in Table 2, we have been able to assign the infrared absorption spectrum of acetone methanesulphonylhydrazone between 40000 and 150cm-1 and to calculate the frequencies of vibration very clearly. Differences between the calculated and experimental values are at worst only a few wavenumbers. Allowing for the fact that the experimental results were recorded on the crystalline solid whereas the calculated values assumed the molecule was isolated we consider the agreement to be satisfactory.
Acknowledgement
The author thanks the UNECSO Global Network for Molecular and Cell Biology (MCBN) for the financial support (Grant No 436).
References
- G. H. Gaozza, J. Med. Chem., 1965, 8, 400.
- N. R. Lomax, V. L. Narayanan, “Chemical Structures of Interest to the Division of Cancer Treatment”, Vol. VI, Developmental Therapeutics Program, National Cancer Institute, Bethesda, MD, 1988.
- P. B. Jensen, B. S. Soerensen, J. F. E. Demant, M. Sehested, P. S. Jensen, L. Vindeloey, H. H. Hansen, Cancer Res., 1990, 50, 3311.
- G. F. Finlay, B. C. Baguley, K. Snow, W. Judd, J. Natl. Cancer Inst., 1990, 82, 662.
- H. Rutner, N. Lewin, E. C. Woodbury, T. J. McBride, K. V. Rao, Cancer Chemother. Rep., Part 1, 1974, 58, 803.
- N. I. Dodoff, Ü. Özdemir, N. Karacan, M. Ch. Georgieva, S. M. Konstantinov, M. E. Stefanova, Z. Naturforsch., B, accepted.
- J. W. Powell, M. C. Whiting, Tetrahedron, 1959, 7, 305.
- PCMODEL, Molecular Modelling Software, Serena Software, Bloomington, IN, 1990.
- N. L. Allinger, J. Am. Chem. Soc., 1977, 99, 8127.
- T. Sundius, “Documentation for the Program MOLVIB (Version 6.0)”, Department of Physics, University of Helsinki, Helsinki, 1991.
- T. Sundius, Commentat. Phys-Math., 1977, 47, 1.
- T. Sundius, J. Mol. Struct., 1990, 218, 321.
- A. Ienco, C. Mealli, P. Paoli, N. Dodoff, Z. Kantarci, N. Karacan, New J. Chem., submitted.
- A. R. Katritzki, R. A. Jones, J. Chem. Soc., 1960, 4497.
- Y. Tanaka, Y. Tanaka,, Chem. Pharm. Bull., 1965, 13, 858.
- K. Hanai, T. Okuda, T. Uno, K. Machida, Spectrochim. Acta, 1975, 31A, 1217.
- K. Hanai,, A. Nocuchi, T. Okuda, Spectrochim. Acta, 1978, 34A, 771.
- R. D. McLachlan, V. B. Carter, Spectrochim. Acta, 1970, 26A, 1121.
- T. Uno, K. Machida, K. Hani, Spectrochim. Acta, 1971, 27A, 107.
- G. Geiseler, G. Hanschmann, J. Mol. Struct., 1971, 8, 293.
- K. Hanai, T. Okuda, K. Machida, Spectrochim. Acta, 1975, 31A, 1227.
- G. Chassaing, J. Corset, J. Limouzi, Spectrochim. Acta, 37A, 721 (1981).
- W. C. Harris, I. W. Levin, J. Mol. Spectrosc., 1972, 43, 117.
- W. C. Harris, D. B. Yang, P. M. Wilcox, Spectrochim. Acta, 1975, 31A, 1981.
- W. C. Harris, S. F. Bush, J. Chem. Phys., 1972, 56, 6147.
- W. C. Harris, I. W. Levin, J. Mol. Spectrosc., 1971, 39, 441.
Received 22nd September 1999, received in revised format 23rd September, accepted 28th September 1999
REF: Dodoff N.I. Int. J. Vib. Spect., [www.irdg.org/ijvs] 3, 4, 7 (1999)

