Infrared Emission Spectroscopy and its application for the characterisation of textile fibres
Marion Friedrich and Dietrich R. T. Zahn
Institut für Physik,
Technische Universität Chemnitz,
D-09107 Chemnitz,
Germany
Email: friedrich [at] physik.tu-chemnitz.de
Introduction
Infrared emission spectroscopy is a commonly known method for the detection of radiation from stars distant from our planet. It is, however, still rarely applied to characterise solid samples on earth. This may be due to the fact that the experiment involves some difficulties which are related to the choice of a suitable reference and the precision of temperature measurements. To date emission spectroscopy investigations have been carried out with samples which are also well suited for conventional reflection or transmission measurements. Such samples are transparent KBr disks [1,2] or thin coatings on metals [2,3,4-7]. However, it is much easier to record absorption spectra than emission ones leading to the rare use of emission spectroscopy. In this study we present an introduction to infrared emission spectroscopy, discuss possible sources of error which may influence the measurements and demonstrate the suitability of emission spectroscopy for the characterisation of textile fibres, i.e. samples without any well-defined sample geometry. Such fibres are thus not suitable for transmission spectroscopy. Of course, it would be possible to prepare KBr pellets, but pellet preparation requires a lot of time and may also be difficult for this kind of material.
First of all, we briefly introduce the relevant formulae, terms and facts which are fundamental to the understanding of emission techniques.
Basics of Emission Spectroscopy
The most important laws describing the emission of radiation are Kirchhoff's law [7] and Planck's formula [8].
According to Kirchhoff´s law, the amount of absorbed and emitted radiation is equal for any body in thermal equilibrium with the environment. If a body is a strong absorber of radiation at a certain wavenumber ![]() (reciprocal wavelength) it is also a strong emitter at that frequency. Its emittance
(reciprocal wavelength) it is also a strong emitter at that frequency. Its emittance ![]() and absorptance
and absorptance ![]() are equal at any temperature T. Emittance and absorptance characteristically depend on the type of sample and its geometry. The emittance
are equal at any temperature T. Emittance and absorptance characteristically depend on the type of sample and its geometry. The emittance ![]() is defined as the ratio of emitted energy of the sample to that of a black body. A black body is a sample which absorbs all incident radiation. Hence from Kirchoff at any temperature, no surface can emit more radiation than a black body i.e. the black body source has the maximum possible emittance
is defined as the ratio of emitted energy of the sample to that of a black body. A black body is a sample which absorbs all incident radiation. Hence from Kirchoff at any temperature, no surface can emit more radiation than a black body i.e. the black body source has the maximum possible emittance![]() . As a perfect emitter the black body serves as a reference standard for the radiative properties of a sample. Its spectral energy density distribution
. As a perfect emitter the black body serves as a reference standard for the radiative properties of a sample. Its spectral energy density distribution ![]() is determined by Planck´s function [3,9,10]
is determined by Planck´s function [3,9,10]
![]() (1)
(1)
with : wavenumber ,![]() : Planck´s constant, c: velocity of light and k: Boltzmann constant.
: Planck´s constant, c: velocity of light and k: Boltzmann constant.
Figure 1 shows the spectral energy density distribution for a black body at different temperatures. With increasing temperature the magnitude of the emitted radiation increases and the maximum shifts to higher wavenumbers. For emission spectroscopy of textile fibres the temperature range from room temperature up to approximately 450K is of interest since the sample temperature must be held below the melting temperature of fibres. From the radiation distribution curves it is obvious that the upper wavenumber limit for the detection of emission spectra increases with the sample temperature. The working temperature of the typical infrared source, i.e. the globar, is at or slightly below 1200K, hence the full range of the mid infrared can be accessed easily. Figure 1 emphasises that we have to measure a signal in emission spectroscopy which is much lower in value than the source signal in absorption spectroscopy and as pointed out above the full frequency range may not be available.
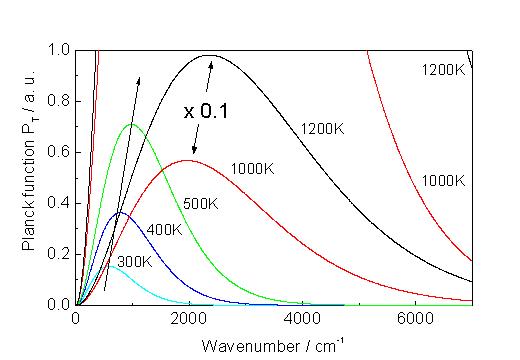
Figure 1. Black body radiation distribution curves calculated for different temperatures.Note that the curves for 1000 and 1200K are reduced by x10
The simplest sample which is as well suited for both emission as for absorption measurements is a flat disk or a substrate covered with a thin film. If such a sample is irradiated by infrared light, the light beam is partly reflected at the surfaces and interface, partly transmitted and partly absorbed by the sample. Neglecting scattering effects the absorptance ![]() can be calculated:
can be calculated:
![]() (2)
(2)
with![]() : absorptance,
: absorptance, ![]() : transmittance,
: transmittance, ![]() : reflectance. Now as we have seen under the same geometrical and thermal conditions the absorptance and emittance of any sample are equal whence Equation (2) for a non-transparent sample reduces to
: reflectance. Now as we have seen under the same geometrical and thermal conditions the absorptance and emittance of any sample are equal whence Equation (2) for a non-transparent sample reduces to
![]() (3)
(3)
The experimental confirmation that equation (3) is valid is presented in figure 2 for a boron nitride film on steel with an optical thickness of 8.6µm. For this film reflectance and emittance measurements were taken. The boron nitride sample is particularly well suited to explain the measurement results. First of all, it is clearly visible that the emittance and reflectance spectra are complementary. Without any measurement error the sum of both should be exactly equal 1 at the same temperature. In the case of our samples some error may be introduced through the fact that the steel substrate was not perfectly polished and that we may not have measured reflection and emission spectra exactly in the same manner. Furthermore, we observe in the emission spectra measured with a DTGS detector a significant increase in noise with increasing wavenumber. As mentioned above the reason is the drastic decrease of the magnitude of the radiation towards higher wavenumber (see Figure 1) characteristic for the low sample temperature used in this experiment [of about 360K]. From both the emittance and reflectance spectra we can conclude that the boron nitride film is hexagonal since very strong features at 800cm-1 and 1400cm-1 marked by in Figure 2 by horizontal lines occur in the spectra. Finally interferences which are useful for the determination of film thickness can be seen in the spectral range above 1700cm-1.
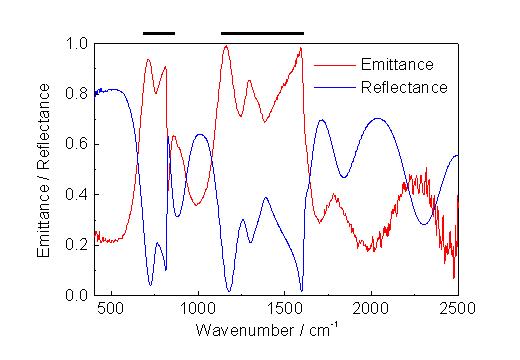
Figure 2. Emittance and reflectance spectra of a boron nitride film on steel.
In the emission experiment we measure the intensity of the radiation radiating from our samples. The resulting so called single beam or single channel spectra contain the information about the optical properties of the emitting sample and its temperature. However, single beam spectra are seriously influenced by the optical design of the spectrometer, the detector used and background radiation, for example from the beamsplitter in the spectrometer. These factors which affect the lineshape of emission spectra as measured by an interferometer are thoroughly described in references [11] and [12]. There an expression is also given for the detected intensity which is valid if the detector temperature is well below the sample temperature TWe will now take a closer look at the measurement procedures and some important factors affecting the final result.
![]() (4)
(4)
where ![]() = instrument response function;
= instrument response function; ![]() =radiation intensity of black body;
=radiation intensity of black body; ![]() = background radiation;
= background radiation; ![]() background radiation reflected off the sample towards the detector;
background radiation reflected off the sample towards the detector; ![]() =reflectance of the sample. In practice it is impossible to avoid the measurement of additional background radiation
=reflectance of the sample. In practice it is impossible to avoid the measurement of additional background radiation![]() . Therefore, special procedures are required in order to select only the characteristic sample properties.
. Therefore, special procedures are required in order to select only the characteristic sample properties.
The method mainly used requires measurements of sample spectra ![]() and black body reference spectra
and black body reference spectra ![]() at two different temperatures [11,13]. From these four measurements the sample emittance can be determined to be
at two different temperatures [11,13]. From these four measurements the sample emittance can be determined to be
![]() (5)
(5)
This experimental method is then well suited if an exact temperature measurement can be performed and a suitable black body reference is available. The advantage is that we do not need to know any special characteristics of our equipment as are described by the instrument response function ![]() in equation (4).
in equation (4).
Complementarily, an interesting method is presented in [14] together with some calculations for the investigation of thin liquid samples using a thick opaque sample of the same liquid as reference instead of a black body, but this is beyond the scope of this paper.
An alternative method is to determine the instrument response function for the experimental setup once and for all. Therefore we substitute in (5) the difference of black body single channel spectra by the product of an instrument response function ![]() and the difference of Planck functions at equivalent temperatures. Since the Planck function is calculated instead of measuring the radiation intensity of a black body the derived response function deviates by a factor including the geometry of experiment from the response function used in equation (4).
and the difference of Planck functions at equivalent temperatures. Since the Planck function is calculated instead of measuring the radiation intensity of a black body the derived response function deviates by a factor including the geometry of experiment from the response function used in equation (4).
Applying equation (3) to substitute also the emittance we get
![]() (6)
(6)
Equation (6) can now be used to determine the response function via reflectance and emission measurement of a reference sample. To minimize errors the reference sample should be a black body. Having the instrument response function ![]() it is then possible to correct measured emission spectra and to determine the emittance
it is then possible to correct measured emission spectra and to determine the emittance![]() .
.
![]() (7)
(7)
As the emittance depends on the temperature, the positions of all characteristic sample features usually shift towards lower wavenumbers with increasing temperature. Furthermore, characteristic features broaden with temperature. At extremely high temperatures the spectra become blurred and look black body-like. For this reason it is important that the temperature difference is not too high if difference methods are applied.
The question arises whether the infrared source in the spectrometer may serve as a reference and consequently make such a complicated procedure obsolete. Indeed it is in principle an almost perfect reference. However, we need to know precisely its radiation characteristic and temperature.
Figure 3 shows the response function of the spectrometer used with a DTGS detector and determined using equation 5. Together with this function the single channel spectrum of the empty spectrometer with globar divided by the Planck function for a source temperature of 1150 K is presented. If the globar would show a black body like behaviour the resulting line shape should be identical to that of the calculated response function. The emittance spectrum of the globar, however, shows two pronounced dips at 470cm-1 and 1100cm-1. These dips on both sides of the Reststrahlenbande of SiC (at 780cm-1) are caused by differences in the globar surface reflectivity. It would be a step forward for a widespread application of emission spectroscopy if the globar emittance curve would be available for taking qualitative measurements routinely with computer assisted black body correction. Due to ageing effects and source temperature variations other methods as the determination of the response function are clearly preferable for quantitative measurements.
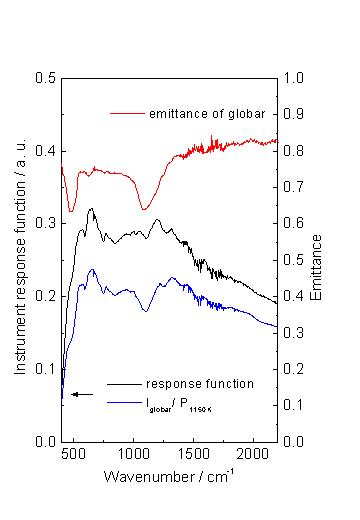
Figure 3. Instrument response function for measurements with the DTGS detector
Emittance of globar at 1150K calculated from the single channel spectrum
Experimental
Determination of instrument response function
Initially investigations were carried out in order to determine the instrument response function ![]() for the Bruker IFS 66 spectrometer used equipped with an emission port. Corresponding to equation (6) it is necessary to take single beam emission spectra at known temperatures for a reference sample under the same optical conditions as used for the emittance determination via reflectance measurement. The ideal reference sample should have both a high emittance and low reflectance and should not show characteristic features. Since the absorptance and also the emittance of any sample depend slightly on the temperature [15] the procedure is only applicable in a limited narrow temperature range.
for the Bruker IFS 66 spectrometer used equipped with an emission port. Corresponding to equation (6) it is necessary to take single beam emission spectra at known temperatures for a reference sample under the same optical conditions as used for the emittance determination via reflectance measurement. The ideal reference sample should have both a high emittance and low reflectance and should not show characteristic features. Since the absorptance and also the emittance of any sample depend slightly on the temperature [15] the procedure is only applicable in a limited narrow temperature range.
We have used a thick non-transmitting pellet of KBr and graphite as reference since its reflectance is much lower than the reflectance of pure graphite [16]. Best results were found for pellets with a medium reflectance between 5% and 6%. Attempts to further reduce the reflectance by decreasing the graphite content of pellets were not successful, because the pellets became more and more transparent, in particular in the lower wavenumber region. For such samples equation (2) becomes invalid. The resulting instrument response function for the DTGS detector is presented in Figure 3.
With this response function the emittance of a flat sample with a large enough area can be calculated using equation (7) where ![]() may be room temperature,
may be room temperature, ![]() the higher sample temperature. If so,
the higher sample temperature. If so, ![]() =0 for the DTGS, because this detector works at room temperature and therefore measures only the net radiation flux. Only if the sample temperature becomes higher than the ambient temperature the detector signal starts to increase.
=0 for the DTGS, because this detector works at room temperature and therefore measures only the net radiation flux. Only if the sample temperature becomes higher than the ambient temperature the detector signal starts to increase.
For quantitative evaluation all measurements have to be done with the same laser frequency or optical velocity of the interferometer mirror as used for the determination of the instrument response function. If this is impossible intensities must be corrected since the detector signal magnitude depends on the measurement conditions. The boron nitride spectrum in Figure 2 is measured applying the procedure described above.
In comparison to the DTGS the MCT detector shows a signal if the sample is held at room temperature. This different behaviour of detectors is caused by the different working temperatures. While the DTGS is in thermal equilibrium with the environment, the cooled MCT detector measures sample and background radiation due to its lower temperature. Owing to the compensation of background radiation terms in the difference of single beam spectra a similar response function can also be derived for different graphite sample temperatures with equation (6) using the MCT detector. In this case we have to consider for the calculation of the Planck function that the detector counts photons.
Characterisation of textile fibres
For these experiments a very simple sample holder was employed, namely a tantalum filament with a diameter of 0.5mm. This heating wire was placed in the focus of the emission port outside the spectrometer IFS 66. The sample, a textile fibre was wound around the wire which was afterwards heated for emission spectroscopy. This simple set-up allowed us to measure emission spectra with the standard DTGS detector. In order to increase the signal intensity a low laser frequency of 2200s-1, corresponding to an optical velocity of 0.139cm/s, was chosen. The infrared radiation was only collected over a small aperture angle of approximately 14 degree which is fixed by the spectrometer optical design. The temperature of the filament was held below 370K. This temperature is low enough to make sure that fibers in contact with the filament do not melt or get otherwise destroyed.
Using the sample holder for fibre samples the calculated emittance spectrum deviates by a factor from the true emittance spectrum. This is caused by differences in the emitting sample areas and their optical projections on the detector area. However, the spectra still reveal only characteristic sample features. Furthermore, some error may occur as a result of filament emission. According to equation (3) the emission of the metallic tantalum filament alone is very low because metals have a very high reflectivity. Therefore the contribution of the wire can be neglected in most applications. But a higher emission can be observed after formation of an oxide layer on the wire.
Another effect which may become important is well known from emission spectroscopy of gases. Self absorption can be observed if the sample temperature decreases locally in the direction towards the detector. The worst case is presented in Figure 4. Spectra 1 and 2 are taken from polyethylene strips with a white painting. The polyethylene strips were wound around the heating wire 2 times. In the first spectrum (black line) the strips are in contact with each other. The second spectrum (red line) shows the result in the case of getting loose. The upper part of the strip is cooler and absorbs the radiation emitted from the strip underneath. We therefore observe dips especially in the main polyethylene peaks at 730cm-1 and 1465cm-1. This effect becomes important whenever absorption is strong as indicated by the difference spectrum 3 in Figure 4. It should be mentioned that fibres wound around the filament only in a single layer yield the best results because commercial textile fibres are thick enough for emission spectroscopy. Moreover, in most cases thinner fibres should result in better spectra.
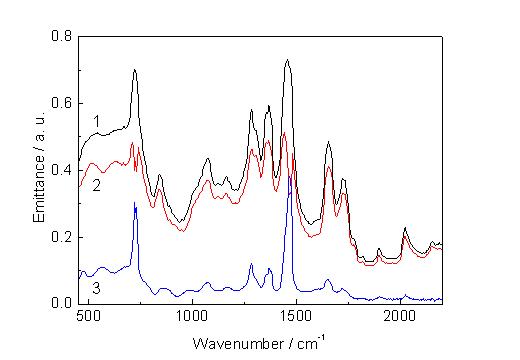
Figure 4. Emittance spectra of Polaren strips covered with a white painting Black line: strips in contact, red line: dips in the main absorption lines due to bad thermal contact are observed, blue line: difference spectrum
Now, after discussing sources of error we present some spectra in order to demonstrate that emission spectroscopy is a perfectly appropriate tool for fibre characterisation
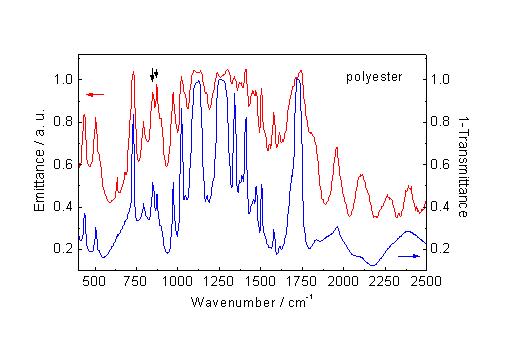 Figure 5. The polyester fibre spectrum (red line) is corrected by a constant factor for comparison to the reverse transmittance spectrum of a 6µm thick polyethylene terephthalate foil (blue line).
Figure 5. The polyester fibre spectrum (red line) is corrected by a constant factor for comparison to the reverse transmittance spectrum of a 6µm thick polyethylene terephthalate foil (blue line).
Figure 5 shows the emittance spectrum of a polyester fibre wound around the heating wire and the reverse transmittance spectrum of a 6µm thick polyethylene terephthalate foil. The polyester fibre emission spectrum shows all characteristic features of polyethylene terephthalate, as can be seen by comparison with the foil spectrum. Small deviations are observed in the intensity ratio for example of the features at 845cm-1 and 875cm-1 marked by arrows. In addition, those features are more dominant in the emission spectra, which are weak in transmission, as a result of a higher effective thickness of emitting material. The dips in the strongest features at 1100cm-1, 1260cm-1 and 1725cm-1 of the emission spectrum are more likely caused by reflection [14] at the fibre-air interface than by self absorption due to a temperature gradient in the sample.
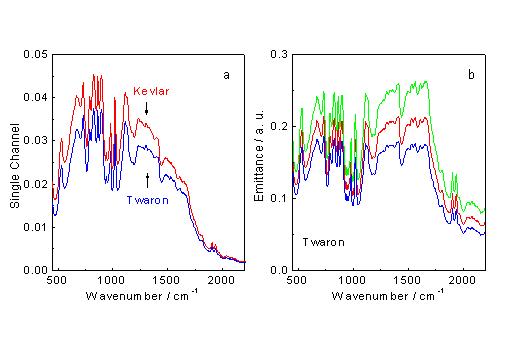
Figure 6. a) Single beam spectra of Kevlar and Twaronb) Effect of temperature correction: T=360K (red line), green and blue lines correspond to ± 10K respectively
Figure 6a shows single beam spectra (corrected by the instrument response function) of commercially available aramide fibres with trade names Kevlar and Twaron. The Kevlar spectrum corresponds well to the micro-emission spectrum of the same material measured by DeBlase and Compton utilising a microscope with MCT detector [8]. Both fibers are fabricated from p-aramide and show therefore the same features.
The influence of black body correction with the difference of Planck functions on the Twaron spectrum is shown in Figure 6b. After correction the features at higher wavenumbers become clearer and more pronounced. Since it is difficult to determine the exact temperature of the fibres we have calculated the emittance spectrum for the most probable temperature and temperatures deviating by ± 10° . All three spectra are well suited for further evaluation. As demonstrated by Figures 7a and 7b we can clearly distinguish by means of emittance spectra between the p-aramide fibres and the m-aramide fibre with trade name Nomex. The spectra measured with the DTGS detector are represented by red lines. The blue curves are emittance spectra from the same samples but measured with the MCT detector. For the same material we observe the same features independent on the detector. The spectral range of the MCT spectrum is limited by the cut off frequency.Figure 6a shows single beam spectra (corrected by the instrument response function) of commercially available aramide fibres with trade names Kevlar and Twaron. The Kevlar spectrum corresponds well to the micro-emission spectrum of the same material measured by DeBlase and Compton utilising a microscope with MCT detector [8]. Both fibers are fabricated from p-aramide and show therefore the same features.
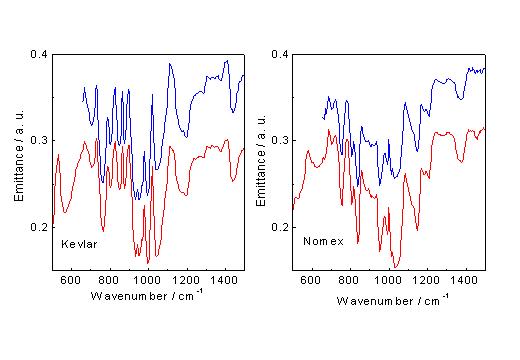
Figure 7. Emittance spectra of Kevlar and Nomex, measured with DTGS (red line) and with MCT detectors (blue line
Summary
We have shown that emission spectra are as characteristic for the sample material as transmission spectra. In the case of fibres, emission spectroscopy has the advantage, that it does not demand any special sample preparation as known from transmission spectroscopy. Good emission spectra of fibres can be observed using a heated wire as sample holder.
It should be useful to collect emission spectra of fibres in a library. Even without such a library a simple comparison with the reverse transmission spectrum as shown in Figure 5 should also yield good results in fibre identification.
References
- P. H. G. Van Kasteren and L. H. Smeets, Proc. SPIE-Fourier Transform Infrared Spectroscopy 289 (1981) 83
- Y. Nagasawa and A. Ishitani, Appl. Spectrosc. 38 (1984) 168
- J. B. Bates, “Infrared Emission Spectroscopy”, in Fourier Transform Infrared Spectroscopy, J. R. Ferraro and L.J. Basile, Eds. (Academic Press, Inc., New York, 1978) Chap. 3, p. 99
- P. Baraldi and G. Fabbri, Appl. Spectrosc. 38 (1984) 668
- M. Handke and N. J. Harrick, Appl. Spectrosc. 40 (1986) 401
- K. Molt, Fresenius Z. Anal. Chem. 308 (1981) 321
- H. A. Willis, “The Infrared Emission Spectrum”, in Laboratory Methods in Vibrational Spectroscopy, H. A. Willis, J. H. van der Maas and R. G. J. Miller, Eds.(John Wiley&Sons, 1991) Chap. 20, p. 473
- F. J. DeBlase and S. Compton, Appl. Spectrosc. 45 (1991) 611 erratum: Appl. Spectrosc. 45 (1991) 1209
- M. Planck, Theorie der Wärmestrahlung (Johann Ambrosius Barth Verlag Leipzig, 1966), 6th ed.
- M. Davies, Infra-red Spectroscopy and Molecular Structure (Elsevier Publishing Company, 1963)
- D. B. Chase, Appl. Spectrosc. 35 (1981) 77
- P. R. Griffiths and J. A. de Haseth, Fourier Transform Infrared Spectroscopy(John Wiley & Sons Inc., New York, 1986)
- D. Kember, D. H. Chenery, N. Sheppard and J. Fell, Spectrochim. Acta 35a(1979) 455
- J. Hvistendahl, E. Rytter and H. A. Æ ye, Appl. Spectrosc. 37 (1983) 182
- B. Buchholz, E. F. Wassermann, W. Pepperhoff, M. Acet, J. Appl. Phys. 75(1994) 7012
- H. R. Philipp, Phys. Rev. B 16 (1977) 2896
REF: Dietrich M. & Zahn D.R.T. Int. J. Vib. Spect., [www.irdg.org/ijvs] 3, 4, 4 (1999)

