Polarised light in Raman Spectroscopy
Anne De Paepe and Editor
University of Southampton
Highfield
Southampton
SO17 1BJ
UK
Raman spectra these days are normally recorded using polarised laser light but the polarisation is usually not used as an asset. We suppose the situation doesn’t differ much from infrared – relatively few infrared users have ever recorded a spectrum through a polariser. In infrared this is a pity because considerable information on molecular orientation can be acquired very easily if you use polarised light. In the Raman much more information is available – read on!
Let’s assume your experiment operates in back-scatter (all F-T Raman accessories do and the microscope instruments (Dilor or Renishaw) also operate in back-scatter. Further, let’s assume your laser is polarised (virtually all of them are) and that you have a sheet of Polarised sheet through which you can record the spectrum. Two experiments are possible on a normal isotropic sample (a liquid, gas or a lump of polymer).
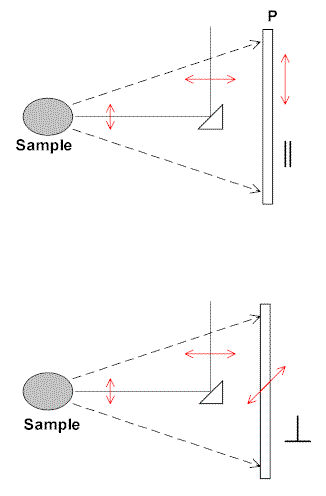
Figure 1. The first experiment is conventionally described as parallel, the second as perpendicular.
The results of the THREE experiments
- No polaroid analyser
- The || experiment
- The experiment
are shown below in Figure 2 for a cuvette of carbon tetrachloride.
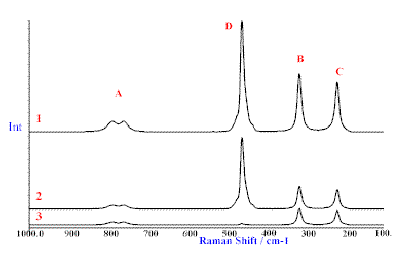
Figure 2. Polarisation experiment carried out on CCl4.
Spectrum 1 was performed without the polaroid analyser.
Spectrum 2 is the || experiment and Spectrum 3, the experiment.
All spectra: 500mW, 10 scans, 4cm-1 resolution.
Raman spectroscopists divide this behaviour into two characteristics. These bands which change in intensity by the ratio ¾ are so called depolarised bands. Those where the intensity ratio is less then ¾ are called polarised bands.So the basic experiment and the parallel one are similar but the perpendicular spectrum is very different. Bands fall into two types – bands A, B and C where the relative intensity of the equivalent bands in experiments 2 & 3 are ¾ and band D where
![]()
is very nearly zero.
So, if we stop there we notice that from a purely analytical point of view Raman spectra can be recorded in two ways in these cases providing twice the specificity of the sample spectrum. As a result, good collections of Raman spectra provide both spectra || & where they can be recorded. This is so in both the Sadtler collection of Raman spectra [1] and also Schrader’s famous collection [2].
We can take the matter further – those vibrations, which take place with the same symmetry as the molecule itself, give rise to the polarised bands. If we look back at the spectrum in Figure 1, above, Carbon Tetrachloride has four modes of vibration only one of which is fully terahedrally symmetrical – the “breathing” mode and it is this that causes the band near 460cm-1.
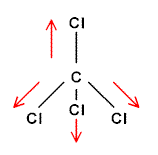
Let us go back to an earlier article your editor wrote telling student readers how to assign Raman spectra to fundamental modes of vibration. The example used was chloroform [3]. The arguments used were based solely on the frequency and intensity of the Raman bands. I also relied on a peculiarity of chlorine containing materials i.e. the fact that chlorine contains two isotopes 35Cl and 37Cl. I could have used polarisation to advantage had I wished to.
In my earlier article the following assignments were made.
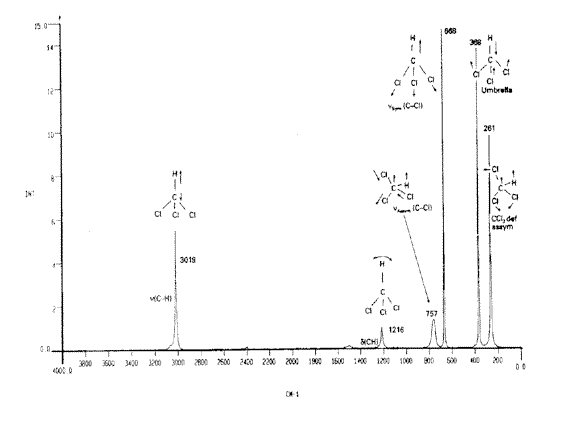
Figure 3. Vibrational assignment for chloroform
In the Figure 4 below, we show the spectrum of CHCl3 recorded with a polarisation analyser and you will see that indeed these three bands are polarised.You will notice that three modes – and three only retain the symmetry of chloroform itself (C3v) vis those at 3019, 668 & 368cm-1.
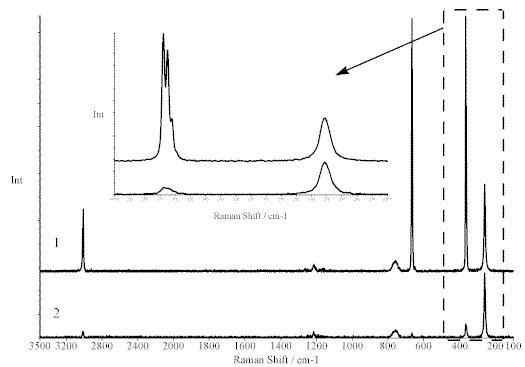
Figure 4. Polarisation experiment carried out on CHCl3.
Spectrum 1 was recorded with the analyser || and Spectrum 2 with the analyser .
All spectra: 500mW, 10 scans, 1 cm-1 resolution
The argument so far is confined to isotropic systems – gases, liquids including solutions and non-oriented solids such as polymers. The reason is purely experimental – the particles and other inhomogeneities scramble the polarised radiation so that it loses its polarisation. There are of course, clear transparent highly oriented specimens such as crystals. These show very complex orientation effects.
Let us again assume the experiment is carried out in backscatter and a crystal is available. A whole series of experiments can be carried out (not just two as described above). Let’s also agree that the crystals can be said to have three orthogonal crystal axes (some crystals have non-orthogonal axes and for the moment we will ignore these). The experiments are drawn below in Figure 5.
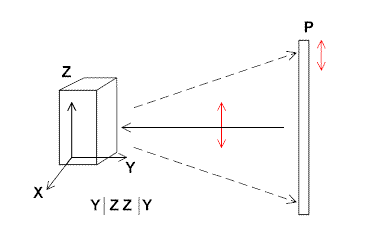
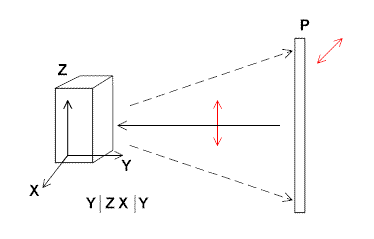
and then the equivalent experiments with the crystal oriented as below
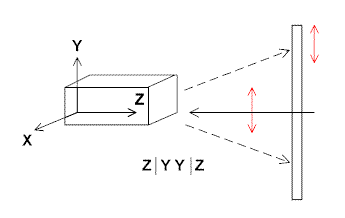
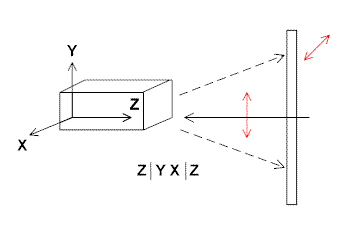
and
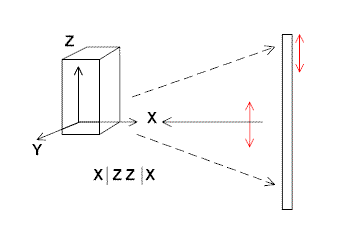
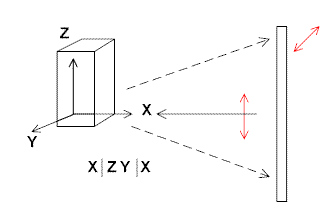
Figure 5.
i.e. 6 different experiments. Obviously, it is somewhat of a nightmare to describe these experiments so Porto many years ago came up with a simple shorthand nomenclature
A| B C | D
A= Direction of laser
B= Polarisation direction of laser
C= Direction of polarisation analyser
D= Direction of view
-all these directions refer to the crystal axes.
The first two experiments above can therefore be labelled. On the left, the laser is entering along axis ‘y’ with polarisation direction along the ‘z’ axis of the crystal. You collect again in the ‘y’ direction and the analyser is set in the ‘z’ direction. So the Porto nomenclature reads- all these directions refer to the crystal axes.
Y | Z Z |Y
We have written the nomenclature in each case next to the drawings above.
Just as we can relate the two Raman spectra described above on isotropic samples to the symmetry of the modes of vibration, the so called ANISOTROPIC experiments on crystals can be used to sort out the assignment of modes of vibration. The differences in the intensities from one experiment to another are considerable so it’s not difficult from the experimental point-of-view to see what is happening. Below in Figure 6 we give an example recorded on a small crystal through a Raman microscope. We will not attempt to explain the spectra here because one needs to understand the theory of the Raman effect and the properties of the polarisation. We will cover this in the near future in another article. If the crystal axes are not orthogonal the situation becomes very complex.
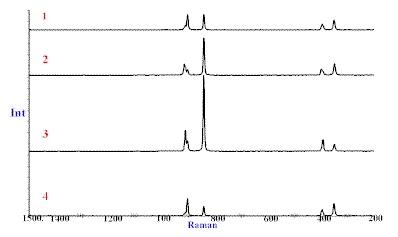
Figure 6. Different polarisation experiments carried out on KMnO4.
KMnO4 are orthorhombic crystals. The space group is Pnma and there are four molecules per unit cell.
In an oriented polymer the orientation is almost invariably cylindrical i.e. the orientation has only one defined axis – say the fibre axis or the axis along which the material was stretched during orientation – not three as in a crystal. So the comparison is as shown in Figure 7.
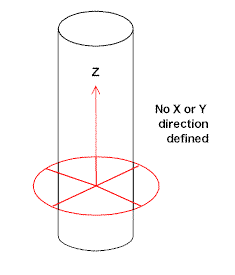
Fibre or polymer film
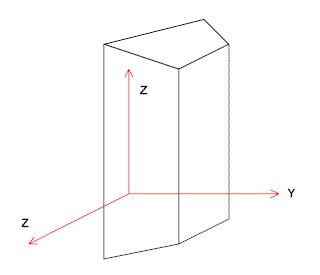
Crystal
Figure 7.
If we apply the anisotropic Raman experiments to a polymer only four differentexperiments can be performed because x & y are interchangeable. We give below in an example, the anisotropic scatter from a highly polyethylene as Figure 8.
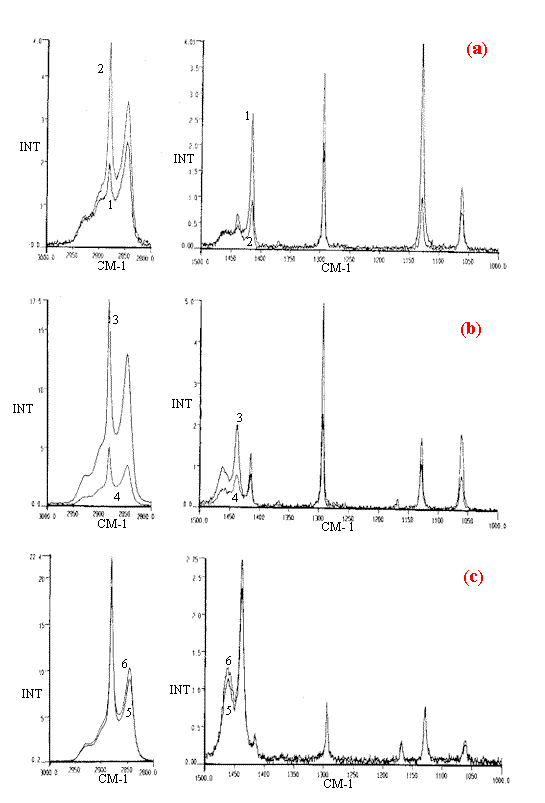
Figure 8. The Raman spectra of ultra-high modulus polyethylene recorded (a) vertical to, (b) horizontal to and (c) along the chain axis. Spectra acquired from 50 acumulations of scans at 1cm-1 res. (laser power = 600mW). Experiments 1, 3 and 5, polariser set vertically; experiments 2, 4 and 6, polariser set horizontally.
See ref [4, 5] for details
Conclusion
Using the information from polarisation on an isotropic sample spectroscopists can obtain twice as much analytical information as they can if they ignore them. They can obtain information on molecular orientation and in crystals they can unambiguously assign their spectra to fundamental modes. Clearly we have not explained all these here – we have only introduced the subject. More will follow in future editions.
References
- Sadtler Standard Raman Spectra. Sadtler Research Labs. Inc., Philadelphia 1976.
- B. Schrader, Raman/Infrared Atlas of Organic Compounds, VCH Weinheim 2nd Edition, 1989.
- P.J. Hendra, Molecular Vibrations – a simple tutorial, IJVS, 2, Ed 3, 1998.
- P.J. Hendra & P. Bentley, Spectrochimica Acta, 51A , (1995), 2125.
- M. Arruebarrena de Baez, P.J. Hendra & M. Judkins, Spectrochimica Acta, 51A, (1995), 2117.

