Neutron Vibrational Spectroscopy
6 Neutron Vibrational Spectroscopy
Stewart F.Parker
ISIS Facility, Rutherford Appleton Laboratory,
Chilton, Didcot, Oxfordshire OX11 0QX, United Kingdom.
E-mail: SFP [at] ISISE.RL.AC.UK
Introduction
Vibrational spectroscopy is commonly used in both industry and academia to provide both quantitative and qualitative information on molecular species and the functional groups present in them. The vast majority of such measurements are carried out using infrared spectroscopy in absorption to directly measure the energies of the vibrational transitions. The other form of vibrational spectroscopy that is commonly encountered is Raman spectroscopy and this is an example of inelastic scattering. With this technique the vibrational spectrum is obtained by measuring the energy difference (gain or loss) between the incident radiation and the small fraction of the radiation that is inelastically scattered. The basic idea when looking for inelastic scattering as a method of measuring the vibrational spectrum is to study the comparison of the energy of incident and scattered photons (Raman spectroscopy), atoms (inelastic helium atom scattering), electrons (electron energy loss spectroscopy and inelastic electron tunnelling spectroscopy) and neutrons (inelastic neutron scattering). It is this latter technique that is the focus of this article. The aim is to give an overview of the practice and uses of inelastic neutron scattering (INS) spectroscopy with examples drawn from research carried out within the last few years with applications to polymers, inorganic chemistry and biology. A very important field for INS spectroscopy is catalysis and this is discussed in the following piece by Hervé Jobic.
7 Neutron properties
The neutron is an atomic particle with a mass of 1.008 amu, almost exactly the same as that of a hydrogen ion (a proton). The neutron is uncharged and only interacts weakly with matter. This means that neutrons are highly penetrating and readily pass through aluminium and steel so suitable cells to allow experiments at extremes of temperature and/or pressure are relatively straightforward to devise. Neutrons are quantum particles and behave simultaneously like particles and waves. Neutrons with an energy equivalent to room temperature (∼200 cm-1) have an associated wavelength of 1.8 Å i.e. on the order of typical interatomic distances in a compound. Probably the most familiar use of neutrons is in neutron diffraction (an elastic scattering process) for structure determination, particularly the precise location of hydrogen atoms. This expolits the wave-like properties; inelastic scattering uses the particle-like properties since the scattering is analogous to the cueball impacting on the pack of reds in snooker. However, the two types of behaviour are inseparable and we make use of diffraction in order to analyse the energy of inelastically scattered neutrons. Neutrons also have a magnetic moment (like a tiny bar magnet) and can be scattered both elastically and inelastically from magnetic centres. This forms the basis for a huge amount of work (primarily by physicists) that is carried out on magnetic materials.
8 Inelastic neutron scattering spectrometers
The prime requirement for INS spectroscopy is a source of neutrons. The two methods of generating neutrons are by shattering nucleii with a high energy proton beam (spallation) or by fission in a nuclear reactor. There are a number of reactor sources around the world [1], the leading one of which is the Institut Laue Langevin (ILL) at Grenoble in France. The world’s most powerful spallation neutron source is the ISIS Facility at the Rutherford Appleton Laboratory (Chilton, UK) Access to such instrumentation requires some planning and of course you have to do the work remotely from your own laboratory and this can be a disadvantage of INS [2].
The two types of source usually operate in different ways; the spallation sources are pulsed while the reactor sources are continuous. This is not an absolute divide: spallation sources can be run continuously and reactor sources can use choppers to run in a pulsed mode. The advantage of using the pulsed mode of operation is that energy analysis can be carried out using time-of-flight techniques (explained later).
9 However they are initially generated, the neutrons are very energetic. They are brought to usable energies by multiple inelastic collisions with a hydrogenous material (a moderator). This provides a means of tailoring the neutron energy to the range of interest since a partial thermal equilibrium is set-up between the neutrons and the moderator. At ISIS the moderators are water (300K), liquid methane (108K) and liquid hydrogen (20K). The type of spectrometer that is used depends on whether the source is pulsed or continuous. With a continuous source, the spectrometer is analogous to a single-beam dispersive infrared spectrometer: the source is a polychromatic beam from which a ‘single’ wavelength is selected by a monochromator, in this case the wavelength dispersion is by Bragg reflection off a single crystal rather than by using a prism or grating, the beam is then scattered by the sample, the scattered neutrons are energy selected by transmission through a beryllium filter and then detected. Beryllium only transmits neutrons of energy less than ∼32 cm-1, the higher energy neutrons are scattered out of the beam and do not reach the detector. The energy scan is accomplished by varying the angle of the crystal in the beam. Now Bragg’s law states:
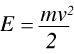 (1)
(1)
since the crystal interplanar distance, d, is constant, the wavelength λ (and hence energy) varies as the angle of incidence θ changes. The energy transferred to the sample, Etrans, is:
![]() (2)
(2)
10 Since the incident and final energies are both known, it is straightforward to calculate the energy transfer. To cover the full range 0 – 4000 cm-1 range a number of different crystal planes need to be used. The instrument IN1BeF at the ILL typifies this type of instrument.
With a pulsed source, the same principle can be used but it is inefficient since most of the neutrons are wasted. An alternative method is to use a broad spectrum beam of neutrons and to use the time-of-flight technique for the energy analysis and it is this method that is employed on the TFXA (and its successor TOSCA) spectrometer at the ISIS pulsed spallation neutron source at the Rutherford Appleton Laboratory. A schematic of the spectrometer is shown in Figure 1. A small fraction of the incident neutrons are inelastically scattered by the sample; those that are backscattered through an angle of 135°and impinge on a graphite crystal. From equation (1), since both d and θ are constant only one wavelength (and its harmonics) will be Bragg scattered by the crystal, the remainder will pass through the graphite crystal to be absorbed by the shielding. The neutrons at multiples of the fundamental wavelength are scattered out of the beam by the beryllium filter which acts as a longpass filter and the remaining neutrons are then detected by the 3He filled detector tubes. The net effect of the combination of the graphite crystal and beryllium filter is to act as a narrow bandpass filter.
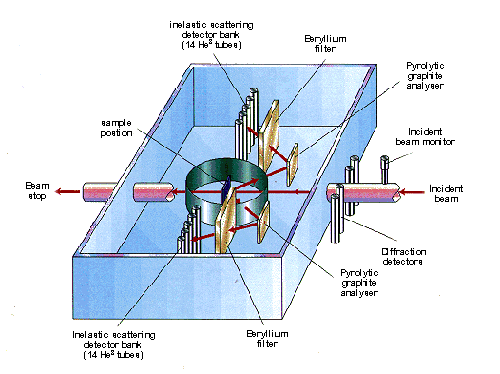
Fig.1 Schematic diagram of the inelastic neutron scattering spectrometer, TXFA
The kinetic energy, E, of a neutron is given by:
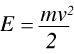 (3)
(3)
where m is the mass of the neutron and v is its velocity. Rearranging (3) gives:
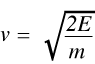 (4)
(4)
and since
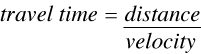 (5)
(5)
It follows that the time of arrival at the detector, T, is the sum of the time from the moderator to the sample, ti, and the time around the analyser tf, thus:
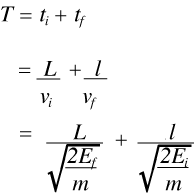 (6)
(6)
Now since the final energy, Ef, the distance round the analyser system, l, and the length of the flight path from the moderator to the sample, L, are all known, it follows that the time of arrival at the detector uniquely defines the incident energy, Ei. and hence the energy transfer at the sample, Etrans. Thus it is a simple matter to convert from time-of-flight to energy. The result is a spectrometer with no moving parts than can record spectra from 0 to 8000 cm-1, although, for reasons that will be discussed later, the best results are obtained below 2000 cm-1. The resolution of the spectrometer is determined by a number of factors but for practical purposes can be taken to be ∼2 – 3% of the energy transfer.
11 Applications of INS
Perhaps the first question that should be asked is: “why use neutrons?” Part of the answer is given in Figure 2. This shows the infrared, 2a, Raman, 2b and INS spectra, 2c of N-phenylmaleimide, a model compound for bismaleimide composites that are used in aerospace applications. It can be seen that all three spectra are very different. There are two main reasons for this. Firstly, whether a mode is infrared and/or Raman active (or is inactive in both) is determined by the symmetry of the molecule. N-phenylmaleimide has 54 normal modes, all of which are Raman allowed, however, seven of the modes are forbidden in the infrared. Note that even when a mode is allowed it may still have little or no intensity in one spectra or the other. In contrast, there are no selection rules for INS spectroscopy and as a result all modes are allowed.
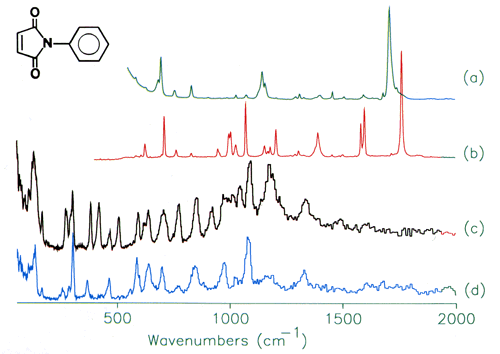
Fig.2 (a) Infrared, (b) Raman, and (c) INs spectra of N-phenylmaleimide. (d) INS spectrum of N-(perdeuterophenyl)maleimide.
Secondly, from studies on related systems, it would be expected that the totally symmetric modes (those where there is no change in dipole moment) would be strong in the Raman and weak in the infrared, vice versa for the asymmetric stretch and deformation modes. These predictions are largely borne out; the strongest band in the infrared spectrum is the asymmetric (out-of-phase) carbonyl stretch at 1707 cm-1, in the Raman spectrum the strongest band is the symmetric (in-phase) carbonyl stretch at 1770 cm-1. However, a number of the modes cannot be located with any degree of certainty in either spectrum. By contrast, the carbonyl bands are completely absent in the INS spectrum, but there are several strong bands that do not have any obvious counterparts in the infrared and Raman spectra and these are the ‘missing’ bands.
The differences arise because the intensity of the ith INS band is proportional to:
![]() (7)
(7)
12 Since neutrons have a mass approximately equal to that of the hydrogen atom, an inelastic collision results in a significant transfer of momentum, Q (ʼn-1), as well as energy, to the molecule. On TFXA (and IN1BeF), the design is such that there is only one value of Q for each energy, (ETrans ≈. 16Q2). (Other instruments at the ISIS Facility and the ILL allow both the energy and the momentum transfer to be varied, but they constitute a different story). Ui is the amplitude of vibration of the atoms undergoing the particular mode. The exponential term in equation (7) is known as the Debye-Waller factor, UTotal is the mean square displacement of the molecule and its magnitude is in part determined by the thermal motion of the molecule. This can be reduced by cooling the sample and so spectra are typically recorded below 50K.
σ is the inelastic neutron scattering cross-section of all the atoms involved in the mode. The scattering cross-sections are a characteristic of each element and do not depend on the chemical environment. The cross-section for hydrogen is ∼80 barns while that for virtually all other elements is less than 5 barns. This means that modes that involve significant hydrogen displacement will dominate the spectrum. This dependence on the cross-section is why the INS spectrum is so different from the optical spectroscopies. There, the intensity derives from changes in the electronic properties of the molecule that occur as the vibration is executed, (the dipole moment and the polarisability for infrared and Raman spectroscopy respectively).
The cross-section is not only element dependent it is also isotope dependent and that of deuterium is ∼5 barns. This can be exploited to ‘eliminate’ parts of the molecule from the spectrum. Figure 2d is again N-phenylmaleimide but with the phenyl ring deuterated. This results in a considerable simplification of the spectrum and all of the modes can be assigned to vibrations of the maleimide ring with the phenyl group treated as a point mass.
Infrared and Raman spectroscopies are frequently called complementary forms of vibrational spectroscopy. Figure 2 strongly suggests that INS should be considered the third leg of the ‘piano stool’ of vibrational spectroscopy.
A very wide range of systems have been studied by INS spectroscopy including: hydrogen in metals [3], catalysts [4], polymers [5], biological samples [6], fullerenes [7] and battery materials [8]. Three examples will be given that illustrate what can be achieved with modern instrumentation.
13 The nine modes of complexed water
When a water molecule is coordinated to a metal atom the three translations and the three rotations of the free molecule become ‘frustrated’ and give rise to six new modes in the complex. Thus a coordinated water molecule has nine vibrational modes associated with it as illustrated in Figure 3 for the [FeCl5(H2O)]2- ion.
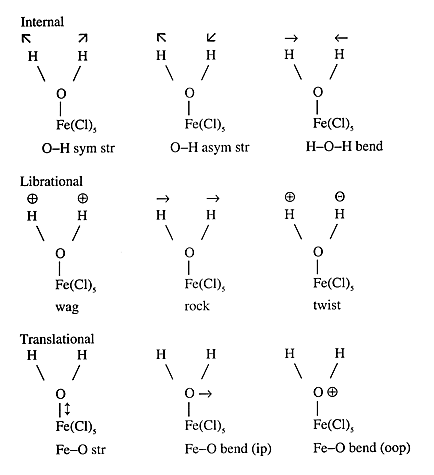
Fig.3 The nine modes of complexed water. Arrows refer to motion in the Fe-OH2 plane, and
to motion perpendicular to the plane (above and below respectively) str stretch, asym asymmetric, sym symmetric, ip in-plane, oop out-of-plane.
Figure 4 show the FT-Raman, infrared and INS spectra of K2[FeCl5(H2O)]. The frequencies and assignments are given in Table 1. Clearly it is the combination of techniques that allows the various modes of coordinated water to be observed since no single spectroscopy shows all of the modes. The internal water stretch modes are best seen in the infrared, since the FT-Raman spectrum shows strong thermal emission in this region + and the INS spectrum is dominated by the phonon wings. A major differences between INS and optical spectroscopies is that in the latter, overtones and combinations are typically ∼1% of the intensity of the fundamental, in INS the intensity can be up to 75% of the intensity! Furthermore, combinations between the internal modes and the external (lattice) modes occur, these are known as phonon wings. As the energy transfer increases, so does the momentum transfer and one of the effects of this is to redistribute the intensity from the fundamental into the phonon wings, shifting the apparent position and considerably broadening it. Both the Debye-Waller factor and this redistribution depend on Q2 and hence Etrans. The resolution is also energy transfer dependent and the combined effect of the three factors is to broaden and attenuate the high frequency features.
+ Editors note – The iron complex absorbs the near infrared laser source and hence heats up. The Raman instrument detects the emmision.
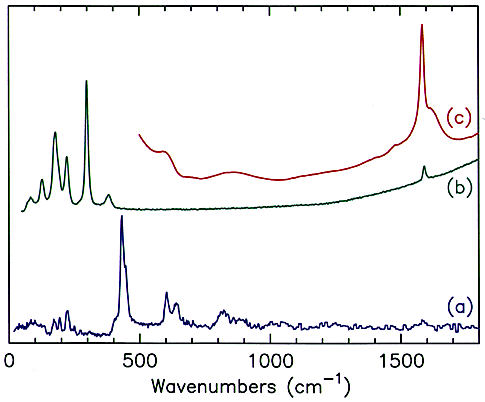
Fig. 4 Comparison of (a) infrared, (b) FT-Raman and (c) INS spectra of K2[FeCl5(H2O)] in the 0 – 1800 cm-1 region.
14 The H-O-H bending mode is observed in both the FT-Raman and the infrared and a weak feature is also apparent in the INS spectrum.
Of the three librational modes, none are visible in the FT-Raman spectra, this region is dominated by the Fe-Cl stretch and bending vibrations. The infrared spectrum shows a weak band at 600 cm-1, in the INS spectrum three modes are visible at 604, 449 and 438 cm-1.These are assigned as the wag, rock and twist respectively.
The translational modes are expected to occur below the librational modes. The Fe-O stretch is clearly seen in all three forms of spectroscopy near 400 cm-1. The remaining two modes correspond to Fe-O bending modes. Since the Fe-O bend is likely to produce a larger amplitude of vibration than the Fe-O stretch (since it is an angular displacement rather than a linear one), the intensity should be at least comparable to the stretch in the INS spectra. The intensity of the band at 222 cm-1 in the INS spectrum would suggest proton motion. There is no obvious candidate for the remaining mode and it is believed that both bending modes are coincident. Note that for a C4v complex (i.e. no hydrogen atoms) the two bending modes are degenerate.
15 Advanced composites
Advanced composites are engineering materials that offer similar mechanical properties to metal alloys but are lighter. The materials consist of fibres embedded in a polymer matrix and there is a need for a spectroscopic technique that can examine the cured resins in the presence of the fibres to aid the understanding of the cure chemistry. The ability to study the reaction(s) is greatly hampered by the nature of the products: they are often highly cross-linked and thus insoluble, and the presence of the fibre matrix makes them difficult to study spectroscopically. Inelastic neutron scattering (INS) has considerable potential in this regard since two common fibre types, glass and carbon, are (almost) invisible to neutrons.
A wide variety of polymers have been used including epoxies, bismaleimides and polyimides. One of the most common polyimides is PMR-15. The chemistry is complex, but consists essentially of two stages; polymerisation to give a norbornene end-capped oligomer followed by reaction of the norbornene group to give the cross-linked polymer. The temperature at which the cross-linking reaction is carried out has a major effect on the mechanical properties of the finished product, particularly its susceptibility to microcracking.
INS spectra of the composites cured at 270 and 330°C are shown in Figure 5a and 5b respectively. There are clearly differences between the two spectra; bands at 1031 and 1114 cm-1 have diminished in intensity and there are indications of changes in the region 200 – 400 cm-1 and at 638, 720 and 1273 cm-1.
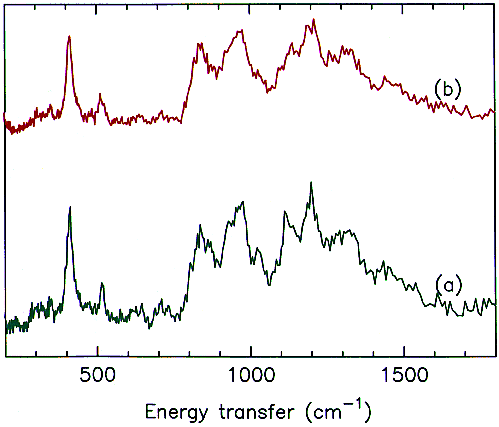
Fig.5 INS spectra of PMR-15 resin carbon fibre composites cured at (a) 270 and (b) 330°C.
16 N-phenylnadimide (see Figure 6 for the structure) has been used very successfully as a model compound for the norbornene endcap and the cross-linking reaction. By deuterating the phenyl ring it is possible to eliminate the spectral features of the phenyl ring and just leave the norbornene endcap. This provides an excellent model compound for the endcap and the spectrum is shown in Figure 6. Comparison of Figure 5 and Figure 6 suggests that the decrease in the 1114 cm-1 and the changes in the 200 – 400 and 600 – 800 cm-1 regions can reasonably be assigned to loss of the endcap. The 1031 cm-1 band does not fit this pattern and may be assigned to the cross-linking.
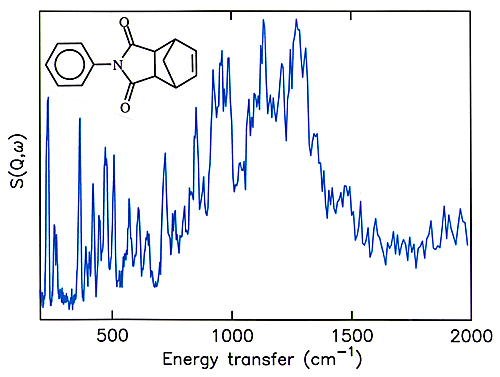
Fig.6 INS spectrum of N-(perdeuterophenyl)nadimide.
17 The examples studied here are particularly difficult samples because as a result of the cure temperatures employed, a significant proportion of the end-groups have already reacted. In addition the composites are only ≈30% by weight resin, of which only 2/7 of the molecules are the end-cap. Nonetheless, as Figure 5 shows, differences between the two samples are apparent. Furthermore, the spectra are characteristic of the bulk of the polymer, in contrast to the infrared methods that only sample the top few microns of the cured composite.
18 Imidazole and zinc tetraimidazole
The metal centres in biological metalloenzymes are frequently found to be coordinated to the amino acid histidine via the unprotected nitrogen of the attached imidazole ring. In carbonic anhydrase, a zinc atom is bonded to three histidine groups and a hydroxyl ligand. An excellent model compound for this is the zinc tetraimidazole complex in conjunction with a non-coordinating counterion. (The structures are shown in Figure 7).
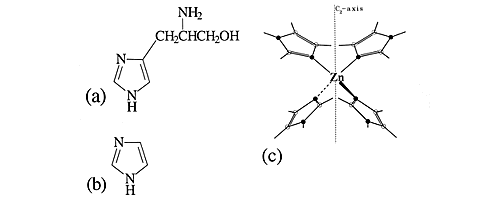
Fig.7 The structures of (a) histidine, (b) imidazole and (c) zinc tetraimidazole. In (c) filled circles are nitrogen atoms, open circles are carbon atoms. One hydrogen atom is attached to each carbon atom and each nitrogen atom that is not bonded to zinc.
19 With INS spectra, the frequencies are determined by the normal modes of vibration, exactly as for infrared and Raman spectra, but the intensities are dependent only on the scattering cross-section, equation (7), and the amplitude of vibration. The latter quantity is calculated as part of the standard Wilson GF matrix method and thus the intensities can be used as an additional constraint in the fitting. This almost doubles the information available without recourse to isotopic substitution. This is in contrast to the optical spectroscopies where the intensities are determined by the electronic properties of the molecule. These are extremely difficult to calculate and require a full ab initio calculation to estimate them. At present this is only practical for small molecules.
The result of a simultaneous fit to all the vibrational frequencies (obtained from infrared, Raman and INS spectra) and the INS intensities of imidazole [9] is shown in Figure 8. It can be seen that the quality of the fit is excellent and this is a direct result of the additional information provided by the INS intensities. The frequencies are obtained with a mean deviation of only 3 cm-1, four times better than that achieved in previous work.
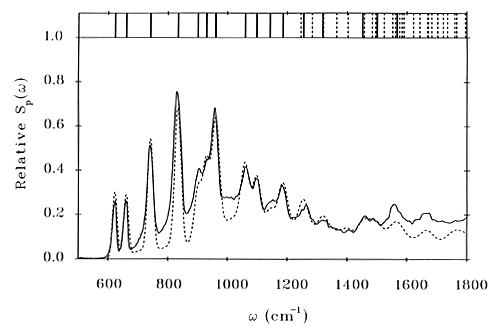
Fig.8 INS spectrum of imidazole (solid line) and the calculated spectrum (dashed line). The top panel shows the frequencies of the fundamentals (solid lines) and the overtones and combinations (dashed lines). Reproduced with permission from: P.W.Loeffen, R.F.Pettifer, F.Fillaux and G.J.Kearley, “Vibrational force field of solid imidazole from inelastic neutron scattering”, Journal of Chemical Physics, 103 (1995) 8444.
20 The force field for imidazole was then used in the analysis of the zinc tetraimidazole [10] complex. Figure 9 shows the evolution of the model used for the low frequency region that contains the skeletal motions of the molecule. These may be roughly categorised as Zn-N stretches, in-plane wags of the imidazole rings, out-of-plane bends and torsions of the imidazole rings about the Zn-N bond. The analysis is complicated by the overlap of the internal and external modes in this region. Nonetheless, the final fit is impressive.
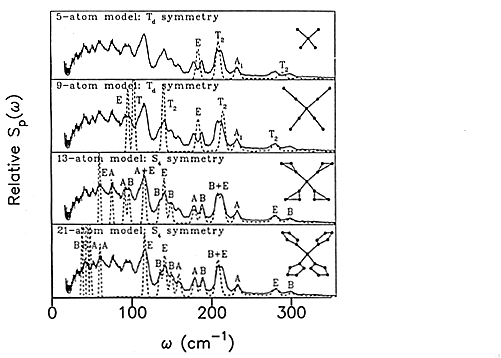
Fig.9 Evolution of the model used to calculate the low frequency spectrum of zinc tetraimidazole. The solid line is the experimental spectrum and the dashed lines are the calculated spectrum using the geometry shown in the right-hand side of each panel. Reproduced with permission from: P.W.Loeffen, R.F.Pettifer and J.Tomkinson, “Vibrational force field of zinc tetraimidazole from inelastic neutron scattering”, Chemical Physics 208 (1996) 403.
21 Future Directions
Crystal ball gazing is always an activity fraught with peril! However, it is possible to highlight a few trends that are becoming apparent. For anybody interested in developing molecular force fields, there is already a strong case to be made that INS spectra are essential for such work. This derives both from the ability to detect vibrations that are either weak or forbidden in optical spectroscopies and the constraint imposed by the need to fit the INS intensities.
For catalyst research, the use of INS to investigate the states of hydrogen on catalysts is already established and will grow. The need to record spectra at low temperature is probably the biggest disadvantage in this area, but, with suitable cell design, there are exciting possibilities for obtaining a ‘snapshot’ of a working catalyst or battery by quenching the process and recording the spectrum, without the need to remove the sample from the reactor.
The work shown here in this article all used TFXA at ISIS. TFXA has just been replaced by a new instrument TOSCA. TOSCA will be installed in two phases, the first phase is identical to TFXA except that where TFXA had two detector banks and a total of 28 detectors, TOSCA has ten detector banks and 150 detectors. This means that there will be major increase in sensitivity. In the year 2000, the second phase of TOSCA will be installed and this will offer a further increase in sensitivity as well as three times better resolution. These advances will drastically reduce the sample measurement time (at present 6 – 12 hours is typical) and so increase the availability of the instrument. There will be greater sensitivity allowing the use of smaller samples, this will be important in biology and biochemistry were it is often difficult to obtain the gram or so of sample needed at present and also for newly developed materials that are only initially available in small quantities. Non-hydrogenous samples can be studied at present but large specimens (5 – 20 gm) are needed. These will become more straightforward in the future. It will also mean that oxide supported metal catalysts with industrially relevant metal loadings (1 – 5%) will be routinely studied.
22 Conclusions
Inelastic neutron scattering spectroscopy is a technique that is still evolving, but has already found widespread applications in physics, chemistry, biology and geology. It is a technique that will always be complementary to other forms of spectroscopy (not least because of the scarcity of spectrometers) and the very high cost per spectrum but the information gained is frequently difficult or impossible to obtain by any other means and add unique insight into the structure and dynamics of the system under study.
References
1 The most up-to-date and useful source of information on neutron scattering centres and their instrumentation is the World Wide Web. The site: http://www.neutron.anl.gov/Neutronf.htm provides an extensive list of websites.
2 Further information about how to obtain access can be found at the ISIS and ILL websites. ISIS is at: http://www.nd.rl.ac.uk/isishome.html and it can contacted by e-mail on: ULS [at] ISISE.RL.AC.UK. Similarly for the ILL, the website is at: http://www.ill.fr/ and it can contacted by e-mail on: SCO [at] ILL.FR.
3 T. Springer and D. Richter, “Hydrogen in metals” in Methods of Experimental Physics (D. L. Price and K. SkÖld, eds.), 23B, Academic Press, San Diego, 1987.
4 J M Nicol, “Chemisorbed hydrogen and hydrogenous molecules”, Spectrochimica Acta 48A (1992) 313.
5 B. Gabrys, D. Hong, F. Nardi, D. G. Peiffer and J. Tomkinson, “Dynamics of sulfonated ionomers in the solid state: inelastic neutron scattering studies”, Macromolecules 26 (1993) 2007.
6 H. D. Middendorf, R. L. Hayward, S. F. Parker, J. Bradshaw and A. Millar, “Vibrational neutron spectroscopy of collagen and model polypeptides”, Biophysics Journal 69 (1995) 660.
7 K. Prassides, H. W. Kroto, R. Taylor, D. R. M. Walton, W. I. F. David, J. Tomkinson, R. C. Haddon, M. J. Rosseinsky, and D. W. Murphy, “Fullerenes and fullerides in the solid state: neutron scattering studies”, Carbon, 30 (1992) 1277.
8 F. Fillaux, C. Cachet, H. Ouboumour, J. Tomkinson, C. Lévy-Clément and L. T. Yu, “Inelastic neutron scattering study of the proton dynamics in manganese oxides”, Chemical Physics 164 (1992) 311.
9 S. F. Parker, K. Shankland, J. C. Sprunt and U. A. Jayasooriya, ‘The nine modes of complexed water’, Spectrochimica Acta A, 53 (1997) 2245.
10 P.W.Loeffen, R.F.Pettifer, F.Fillaux and G.J.Kearley, “Vibrational force field of solid imidazole from inelastic neutron scattering”, Journal of Chemical Physics, 103 (1995) 8444.
10 P.W.Loeffen, R.F.Pettifer and J.Tomkinson, “Vibrational force field of zinc tetraimidazole from inelastic neutron scattering”, Chemical Physics 208 (1996) 403.
REF: Int. J. Vib. Spect., [www.irdg.org/ijvs] 2, 1, 6-22 (1998)
