Neutron Spectroscopy in Catalysts
H.Jobic
Institut de Recherches sur la Catalyse,
CNRS
2 Avenue Albert Einstein,
69626 Villeurbanne
France
Introduction
Because of its penetration power, the neutron does not act as a surface probe. However it is possible to obtain spectra of surface species provided that the adsorbate has a considerably larger neutron scattering cross section than the substrate. Since the hydrogen atom has the largest neutron scattering cross section, (see the paper by S.F.Parker), it is this that is the preferred probe for adsorption studies.
INS is one of several vibrational techniques available for us to probe surface phenomena. Each technique has its own particular advantages for a given system in terms of spectral domain, resolution, sensitivity and experimental conditions. For example, infrared spectroscopy is a very efficient method to detect adsorbed CO but it is much less sensitive to adsorbed hydrogen.
The applications of INS to catalysis have mainly focused on systems which are either difficult or impossible to study by other spectroscopies. This arises where the sample is almost opaque or even completely black so that it may have only limited frequency windows in infrared similarly the sample may decompose or fluoresce in the laser beam in Raman. Comparisons have been made in a few cases between INS and the results obtained by electron energy loss spectroscopy (EELS).
Real catalysts, supported or unsupported, can be tackled by neutron scattering. These catalysts have generally inhomogeneous surfaces, e.g. oxides, sulphides and metals, although zeolites, which are well-crystallised materials, are well suited to the method. These substrates can be almost transparent to neutrons if they contain only a small quantity of hydrogen, in which case the neutron spectrum will be fairly flat and it will be possible to observe all the vibrational modes of the adsorbate.
24 Examples
As applications of INS to catalysis, one can mention studies concerning hydrogen chemisorbed on metals, sulphides and oxides, or hydroxyl groups; organometallic compounds; hydrocarbons and water on different catalysts and zeolitic systems. Some recent examples will now be described. The spectra were recorded with the IN1BeF spectrometer at the Institut Laue-Langevin (Grenoble, France), or with the TFXA spectrometer at ISIS (Rutherford Appleton Laboratory, UK).
25 1. Hydrogen chemisorption
Hydrogen chemisorbed on high surface area materials is difficult to characterise by optical spectroscopies. EELS data have been obtained on single crystals and since only a limited number of sites are available on well-defined crystal planes, the results have turned out to be useful for assigning the spectra obtained from polycrystalline materials.
With INS, all the local modes of hydrogen can be observed because there are no selection rules, which is clearly an advantage. However, if there are different planes exposed on the surface or if there are several species adsorbed, the assignment can be more difficult.
1.1. Hydrogen on nickel
If we consider for example hydrogen on nickel powders, all the recent INS studies indicate that hydrogen is predominantly multiply bonded, under (µ3-H) form [1-3]. Hydrogen is indeed predominantly multiply bonded to metal surfaces, this has been found by many experimental and theoretical methods. Intuitively, hydrogen tends to maximise its interaction with the surface. Here is a design of the 2 modes:
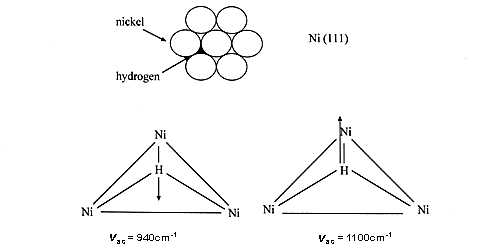
26 However, some authors still claim that after dissociation one hydrogen atom is only bonded to a single nickel atom (e.g. ref. 4), in complete disagreement with theoretical and experimental results, including the work on single crystals.
In the first INS studies on Raney nickel [1-2], the catalyst was outgassed at a sample temperature of 573 K, and it was clear from INS that no hydrogen was left on the surface. However, sintering occurs under these conditions and the surface area was found to decrease from 130 down to 40m2g-1.
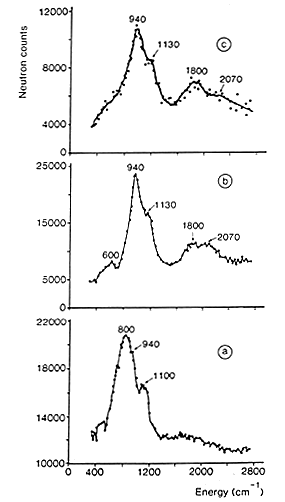
Figure 1: INS spectra of hydrogen adsorbed on a doped Raney nickel [3]:
(a) residual hydrogen, after desorption at 373 K.
(b) spectrum obtained after adsorption under 13 mbar of H2 (the spectrum of residual hydrogen has been subtracted).
(c) spectrum obtained after adsorption of H2 at atmospheric pressure (spectra a and b have been subtracted).
27 The spectrum shown in Fig. 1(a) was obtained after outgassing at only 373 K. The signal produced by the aluminium container and the phonons due to the nickel sample have been subtracted. INS intensities show that a large quantity of hydrogen is present on this catalyst, about 30% of the amount originally adsorbed (this quantity depends on the pumping rate). At this temperature (100°C), no structural modification is induced but water has been completely removed. The spectrum of residual hydrogen consists of two bands at 800 and 1100 cm-1 sitting on a large background. The background is due to the broad distribution of sites for hydrogen. Even if the surface is mainly made of low index planes, the surface is far from being perfect: defects, steps, and kinks are known to occur. The two modes at 800 and 1100 cm-1 were assigned to the antisymmetric (E) and symmetric (A) stretching modes of hydrogen atoms adsorbed on sites of nearly C3v symmetry, located on the (110) faces. The weaker contribution observed at 940 cm-1 was assigned to hydrogen adsorbed on C3v sites, on (111) faces (See above).
28 The two modes of this species are more clearly observed in Fig. 1(b) which corresponds to the spectrum obtained after adsorption under an equilibrium pressure of 13 mbar of H2. The contribution from residual hydrogen has been subtracted and hence the base line is close to zero. The band at 940 cm-1 is assigned to the E mode of hydrogen adsorbed on C3v sites, while the shoulder at 1130 cm-1 corresponds to the A stretching mode. The overtones and combination of these two modes produce a broad contribution around 2070 cm-1. The band centred at 1800 cm-1 is assigned to the stretching mode of on the top hydrogen (a hydrogen bonded to a single Ni atom).After hydrogen adsorption under atmospheric pressure, and subtraction of all the previous contributions (spectra a and b), the spectrum shown in Fig. 1(c) is obtained. The main species we see is still the one located on C3v sites, but the relative intensity of the band at 1800 cm-1 has increased.
In conclusion, after evacuation of the Raney nickel at 373 K, 30% of the total hydrogen uptake remains on the surface. This residual hydrogen is adsorbed on (110) and (111) faces, and also on defects. The top layered hydrogen is only detected upon readsorption of hydrogen, at higher pressure. This shows that multiply bonded hydrogen is more strongly adsorbed than linear hydrogen. This species appears close to the saturation of the surface. Even if the proportion of linear hydrogen is small (about 15%), it could be the active species in hydrogenation reactions since it has been found from kinetic studies and pulse experiments that only weakly adsorbed hydrogen is active for hydrogenation of acetonitrile [3].
29 1.2. Hydrogen on ruthenium sulphide
This is a very important technological area. Sulphide catalysts (MoS2 based) are used in almost every refinery in the world, essentially to remove sulphur and/or nitrogen from hydrocarbons and to hydrogenate petroleum, e.g. aromatics to cycloakanes.
RuS2 is 15 times more active that MoS2 in hydro desulphuration of dibenzothiophene and 6 times more active in hydrogenation of biphenyl. It has been postulated that hydrogen may be adsorbed either homolytically or heterolytically. On sulphides, accordingly, hydrogen chemisorption should form not only SH groups but also metal-hydrogen bonds. Hydroxyl and sulphhydryl groups have previously been measured but hydride-type hydrogen has never been clearly identified. In particular MoH species have not been observed on MoS2 in spite of several INS experiments.
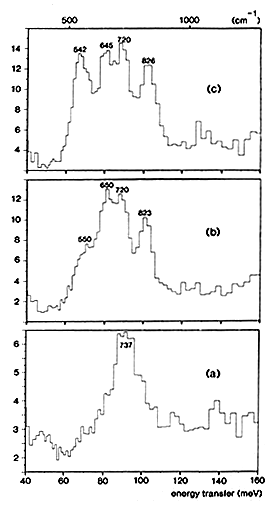
Figure 2: INS spectra obtained at 25 K with ruthenium sulphide:
(a) unreduced catalyst.
(b) 2. hydrogen adsorbed at low pressure (less than 1 mbar) on partially desulphurised RuS2.
(c) hydrogen adsorbed at higher pressure (0.5 bar at 295 K) on partially desulphurised RuS2.
30 The interaction of hydrogen with RuS2 has been recently studied by INS [5] because this sulphide is ˜10 times more active than MoS2 in hydrogenation and hydrodesulphurization reactions. This could be due to the larger adsorption capacity of ruthenium sulphide or to the presence of different hydrogen species. Unsupported RuS2 consisting of homodispersed spheres with a diameter 45-50 Å was used. By changing the degree of reduction and the experimental conditions, several hydrogen species have been observed:
(i) When the catalyst is sulphided at 673 K under H2S flow, chemical analysis gives a stoichiometry S/Ru = 2.25. The INS spectrum shown in Fig. 2(a) indicates only the presence of SH groups on the surface. The peak measured at 737 cm-1 is assigned to SH bending modes, in agreement with previous INS studies performed on other sulphides: these modes were measured at 694 cm-1 on WS2 [6] and at 650 cm-1 on MoS2 [7].
(ii) If the catalyst is partially desulphurized under H2 flow at 513 K, the solid composition becomes RuS1.88. After hydrogen adsorption at low pressure (less than 1 mbar), a new peak and a shoulder appear respectively at 823 and 550 cm-1, Fig. 2(b). When the hydrogen pressure is increased (0.5 bar at 295 K), the peak at 542 cm-1 gains further in intensity, Fig. 2(c). This peak and the one measured at 826 cm-1 are assigned to the bending modes of two different RuH species. It appears that the hydridic group which gives rise to the peak at 542 cm-1 is more weakly adsorbed than the species which yields the peak at 826 cm-1. Since it has been mentioned in the previous section that on Raney nickel, reactive hydrogen is the more weakly adsorbed species, it can be proposed that the hydrogen species active on ruthenium sulphide for hydrogenation reactions is the one giving rise to the peak at 542 cm-1.
Since the integrated intensities of the bands are a direct measure of the populations of the various species, it can be concluded that the reduction of the catalyst creates new SH groups: their intensity is ˜3 times larger in Fig. 2(b) than in Fig. 2(a). The shift to lower frequency observed for the SH modes after reduction, from 737 to ˜683 cm-1, indicates that the Brönsted acidity of the catalyst increases.
31 2. Water in interaction with acidic sites in zeolites
A question which is much debated at the moment is whether the Brönsted acidity of several solids, e.g. zeolites or sulphated zirconia, is high enough to protonate water. Two possible structures have been envisagedÝ: a hydrogen-bonded water molecule and a protonated molecule, H3O+, the hydroxonium ion. Most of the experimental results have been obtained by NMR or infrared spectroscopies, but the interpretation of the results is complicated. In NMR, rapid exchange can take place at room temperature between molecules in different adsorption states. In infrared, there are resonant interactions in the stretching OH region with overtones of OH deformations.
Recent ab initio calculations performed on small clusters indicate that only the hydrogen-bonded structure is a minimum whereas the hydroxonium species is a transition structure for proton transfer [ 9]. However the energy difference between the two structures is small, a few kJ/mol.
Here, the comparison between INS and theoretical calculations is fruitful. INS spectra can be simulated for the two possible water structures using theoretical frequencies and atomic displacements as inputs [8]. The two calculated spectra are compared with the experimental data in Fig. 3.
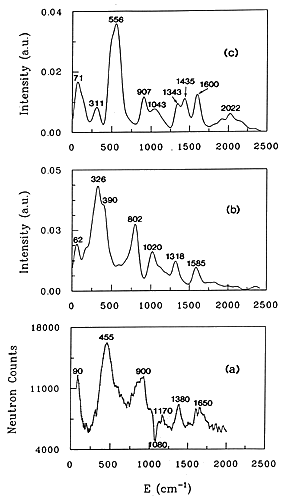
Figure 3. INS spectra of water adsorbed at low loading in H-ZSM-5
(a) experimental spectrum
(b) spectrum simulated for a water molecule hydrogen-bonded to a bridging hydroxyl group.
(c) spectrum simulated for a hydroxonium ion.
32 The experimental INS spectrum, Fig. 3(a), corresponds to a ratio H2O/H+ of 0.61 in the H-ZSM-5 zeolite. The contribution from the dehydrated zeolite has been subtracted which explains the negative peak at 1080 cm-1. This band corresponding to d(OH) deformations of the acidic groups. The negative contribution in the difference spectrum indicates interaction of water with the acid sites. In the case of water interaction with acid sites in zeolites, ab initio calculations give the frequencies and the atomic displacements so that INS spectra can be calculated without adjustable parameters. For larger systems: benzene in NaY, ab initio calculations are not possible so that the frequencies and the atomic displacements have to be derived from empirical force fields calculations. To compare experimental and simulated spectra, they can be superposed one on top of the other, as in Figure 3; the comparison is made by eye. The second method is to fit the force field directly to the observed INS profile.
The two calculated spectra are shown in Figs. 3(b) and (c). It is worth noting that there are no adjustable parameters, only the resolution function has been introduced. It is clear from a comparison of the spectra in Fig. 3 that the hydrogen-bonded water model, Fig. 3(b) reproduces better the experimental profile than the hydroxonium model, Fig. 3 (c).
The only deficiency in the simulation is that the calculated frequencies are situated ˜80 cm-1 too low in energy. Ab initio quantum calculations yield harmonic vibrational frequencies systematically shifted with respect to the observed frequencies. Therefore the calculated frequencies have to be scaled by a value ranging from 0.8 to 1.1. The assignment of the main INS bands is however simple. The band measured at 1650 cm-1 is assigned to the bending of the water. The peak at 1380 cm-1 corresponds to the perturbed deformation mode of the acid site, δ(OzHz). The band having a maximum at 900 cm-1 corresponds to the out-of plane deformation of the proton hydrogen-bonded to the zeolite: δ(OwHb). The largest peak at 455 cm-1 is the sum of several contributions: the out-of-plane deformation of the free water proton, δ(OwHf) and intermolecular modes of water (twisting and rocking). Translational modes of water give a band at 62 cm-1 in the calculated spectrum, compared with 90 cm-1 in the experiment.
33 3. Benzene adsorbed in NaY zeolite
Ab initio calculations are not very often available to simulate INS spectra without adjustable parameters. Generally, a quantitative interpretation is based on an empirical force field. The first approach was to compare visually observed and calculated spectra to test the vibrational assignment. At a later stage [10], a method was proposed by which the vibrational analysis is performed by the refinement of the force constants to give a least-squares fit of the calculated spectrum to the observed profile.
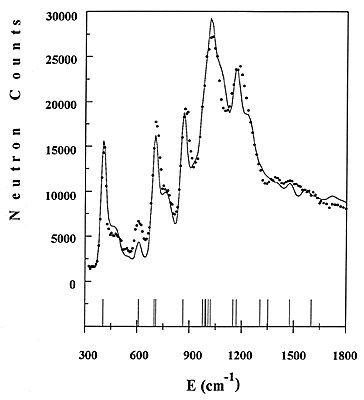
Figure 4: Comparison of experimental and calculated INS spectra of benzene adsorbed in NaY zeolite.
An example concerning benzene adsorbed in NaY zeolite will be given here [11]. Part of the experimental spectrum, obtained for a loading of one molecule per supercage, is shown in Fig. 4 as a dotted line. The frequencies of the fundamentals are indicated as sticks. Side bands due to combinations with the external modes can be measured in between fundamentals.
34 The force constants of adsorbed benzene were refined directly to the observed profile, starting from a reasonable force field. The refinement includes the intensities from fundamentals, overtones and combinations, the contributions from all atoms being added up. The calculated profile is shown in Fig. 4 as a continuous line. The agreement with the experimental data is reasonable. Not all the frequencies are resolved, but the method of treating overlapping modes is similar to the Rietveld method # in powder diffraction. The entire INS profile is refined, instead of just adjusting the frequencies of the normal modes. The frequencies of all fundamentals are thus obtained, whereas they have to be derived from overtones or combinations bands in infrared.
It appears that much progress has been made in the data treatment of the INS spectra, since the first quantitative interpretation of benzene [12]. In former times, the instrumental resolution was low and only the intensities from the fundamentals were calculated. The experimental spectra can be now simulated with a good accuracy because the resolution varies with the energy transfer. At the present time, it is of ~10 cm-1 (FWHM) at 200 cm-1, rising to 30 cm-1 at 1500 cm-1
#The Rietveld method is used for X-ray or neutron diffraction with powders (as opposed to single crystals). With a powder, there is usually overlap between adjacent peaks, so that individual reflections cannot be measured. This produces a complex diffraction profile that is calculated from an initial structural model as a sum of overlapping reflections. It is then compared to the observed pattern, assuming a peak-shape function. By varying the unit-cell parameters and the atomic parameters (positions, occupancies, Debye-Waller factors…), the best least-squares fit between observed and calculated profiles can be obtained, and hence the `best’ crystal structure is refined.
35 Conclusion
The information that is extracted from the INS results cannot usually be obtained from other vibrational methods. INS is well suited to characterise different adsorbed hydrogen species or the Bronsted acidity of a catalyst. The nature of adsorbed molecules can also be identified and the adsorption geometry and strength of bonding can be determined. In the future, quantitative interpretations will be more common, to use the information contained in the intensities. However the small number of high resolution spectrometers (only four in the world) will always limit the number of applications to highly selected systems.
References
1 Jobic H. and Renouprez A., J. Chem. Soc., Faraday Trans. I 80 (1984) 1991-1997.
2 Jobic H., Clugnet G. and Renouprez A., J. Electron Spectrosc. Rel. Phenom. 45 (1987) 281-290.
3 Hochard F., Jobic H., Massardier J. and Renouprez A., J. Mol. Catal. A 95 (1995) 165-172.
4 Richardson J. T. and Cale T. S., J. Catal. 102 (1986) 419-432.
5 Jobic H., Clugnet G., Lacroix M., Yuan S., Mirodatos C. and Breysse M., J. Am. Chem. Soc. 115 (1993) 3654-3657.
6 Wright C. J., Fraser D., Moyes R. B. and Wells P. B., Appl. Catal. 1 (1981) 49-58.
7 Sundberg P., Moyes R. B. and Tomkinson J., Bull. Soc. Chim. Belg. 100 (1991) 967-976.
8 Jobic H., Tuel A., Krossner M. and Sauer J. J. Phys. Chem. 100 (1996) 19545.
9 Krossner, M. and Sauer J., J. Phys. Chem. 100 (1996) 6199-6211.
10 Kearley, G. J., J. Chem. Soc., Faraday Trans. 2 82 (1986) 41-48.
11 Jobic H. and Fitch A. N., Progress in Zeolite and Microporous Materials, Studies in Surface Science and Catalysis, Vol.105A, H. Chon, S. K Ihm and Y. S. Uh, Eds. (Elsevier, 1997) pp. 559-566.
12 Jobic H., Tomkinson J., Candy J.P., Fouilloux P. and Renouprez A. Surface Science 95 (1980) 496-510.
REF: Int. J. Vib. Spect., [www.irdg.org/ijvs] 2, 1, 23-35 (1998)
