Background to the use of Specular Reflection and Reflection/Absorption Methods
31. Background To The Use Of Specular Reflection And Reflection/Absorption Methods
Dr W.Maddams
Specular Reflection
In his article Dr. Spragg points out two facts which provide the basis for the measurement of infrared spectra using specular reflection methods, in which the angle of incidence on the sample surface is equal to the angle of reflection from it. The first is that the intensity of reflection is a function of the refractive index of the medium at which reflection occurs. For normal incidence the fraction of the radiation that is reflected is (n-1)2/(n+1)2, where n is the refractive index of the medium, and the radiation is incident through air, whose refractive index is 1.0 for practical purposes. Secondly, the refractive index changes appreciably in the vicinity of an absorption band, passing through a minimum on the high wavenumber side of an absorption band and a maximum on the low wavenumber side. These two facts will now be considered in rather more detail because they are central to the successful use of the specular reflection technique.
32. The change in refractive index with wavelength for a given material, which is known as its dispersion, is responsible for several well known effects in the visible spectral region. The most striking of these is the rainbow. In the case of most compounds, including water, the refractive index increases in passing from the red to the blue end of the visible spectrum so that sunlight, in passing through raindrops, has its constituent wavelengths spread out, giving a bar with its inner edge violet and the outer edge red. The separation of sunlight into its constituent wavelengths by a glass prism was first reported by Sir Isaac Newton. Here also, the deviation of the violet end of the visible spectrum is greater than that of the red end because the refractive index of glass increases with decreasing wavelength.
In the infrared spectral region, simple optical materials such as sodium chloride and potassium bromide, which are transparent over much of the spectral range useful for structural diagnostic work, behave in the opposite manner. Their refractive indices increase with increasing wavelength, and the rate of increase also increases with increasing wavelength. It is for this reason that the infrared spectrometers of some forty or fifty years ago, which used sodium chloride prisms, had rather poor resolving powers at 3000cm-1 but were very adequate in the vicinity of 700cm-1.
What, then, is the reason for the change in refractive index with wavelength and why does it occur in opposite directions with respect to wavelength in the visible and infrared spectral regions? The answer, in its simplest form, is provided by the behaviour of the materials commonly used to make dispersing prisms for the two wavelength ranges. In the case of glass it becomes increasingly opaque, as the result of absorption, in moving from visible wavelengths to those in the near ultraviolet region. The same is true of quartz, which is transparent to somewhat shorter wavelengths. In the infrared region, sodium chloride becomes increasingly opaque as 15µ (650cm-1) is approached and the relevant value for potassium bromide is about 25µ (400cm-1). Clearly, the refractive index change is to be associated with the onset of absorption.
33. In the ultraviolet/visible region the absorption results from changes in the electronic energy levels. These changes occur at lower energies, and hence give absorption at longer wavelengths, for compounds where some electrons are more loosely bound, e.g. the π-electrons in aromatic compounds. Hence, in the visible spectral region, particularly at the blue end, the refractive index of benzene increases more rapidly with decreasing wavelength than that of n-hexane, and its dispersion is correspondingly greater.
In the infrared spectral region, molecular vibrations are responsible for the absorption of energy. With sodium chloride and potassium bromide the absorption only occurs at relatively long wavelengths so their refractive indices and dispersions increase unidirectionally over the range commonly used for analytical purposes. However, organic compounds in general have an appreciable number of vibrational modes, and hence absorption bands, over the mid-infrared spectral range. There will therefore be refractive index changes in the vicinity of each of these bands, as noted by Dr. Spragg. Consequently, the reflection coefficient will change in a rather complex way as a function of wavelength, but one which will contain information on these absorption bands.
34. In order to formulate this process mathematically, it is necessary to modify the simple concept of refractive index and work in terms of what is known as the complex refractive index ñ, defined as ñ=n+ik. Here, i is the square root of -1 and k is an absorption coefficient which is related in a simple mathematical way to the familiar molar absorption coefficient. Hence, at normal incidence, the fractional reflection becomes (ñ-1)/(ñ+1)2 and its variation with wavelength contains information about the variation of k with wavelength.
35. However, the interpretation of a reflection spectrum is not particularly straight- forward mathematically. Kronig, in 1926, and Kramers in 1929, developed the required theory in terms of what are known as integral equations. These equations also include the effect of varying the angle of incidence, for a given value of ñ. The coefficient of reflection is a function of this angle and increases rapidly to a value of unity as the angle approaches 90°, the condition known as grazing incidence. The Kramers and Kronig equations were not put to practical use for about half a century, for two reasons. Until the development of FTIR spectrometers reflection spectra of adequate intensity and signal to noise ratio were difficult to obtain. Secondly, the calculation of the required spectrum from the experimental reflection measurements was impossibly time consuming, until the advent of modern fast and compact computer systems. Serendipitously, the computer unit required for the Fourier transform operation is equally adept at coping with the reflection calculations via what is universally known as the Kramers-Kronig transformation. Efficient algorithms for this transformation are now available and they form part of the software package of present day FTIR spectrometers. Spectra of the type shown in Fig.2 of Dr. Spragg’s article may now be obtained routinely (see Paragraph 19).
36.Reflection-Absorption Spectroscopy
In the situation considered thus far the intensity of the radiation reflected at the surface of the sample is measured over a chosen wavelength range and this yields the absorption spectrum, after a mathematical transformation, because the reflection coefficient contains a wavelength dependent terms related to the absorption coefficient of the sample. A proportion of the incident radiation will pass into the sample by the process of refraction and some of this will be absorbed. However, if the sample is homogeneous and there is no scattering, none of the attenuated beam will emerge from the sample in the direction of the reflected radiation. Hence, sample absorption is irrelevant.
37. However, if the sample is in the form of a comparatively thin layer on a reflecting substrate, as is the case with coatings on metal cans, some of the radiation which has entered the sample will suffer loss by absorption, then after reflection at the substrate will return towards the surface, losing more intensity in the process and exit the sample with the radiation reflected at the surface. The outcome will be a spectrum in which the observed peaks derive part of their intensity from the specular reflection process and part from conventional absorption. The optimisation of the intensity of such spectra, for a given sample thickness, involves the angle of incidence both directly and indirectly, the latter because at near-normal incidences standing waves occur at the surface.
Standing waves, or stationary waves as they are sometimes called, may occur with any type of longitudinal wave motion but are most easily demonstrated in terms of transverse waves sent down a taut horizontal cord, fixed at one end and hand held at the other, as shown in Fig.1a. Upward and downward movement of the hand generates a longitudinal wave, which is reflected back when it meets the fixed end. If the hand is moved at random there is confused movement of the cord, in which progressive waves in both directions occur for short intervals on a random basis. However, if the movement of the hand is suitably timed the cord appears to vibrate transversely as a whole, with no sign of a progressive wave. This is what is termed a standing wave. Figs. 1b, 1c and 1d show three such standing waves, whose wavelengths are in the ratio 3:1.5:1. It follows that the frequencies of these waves must be in the inverse ratio 1:2:3. When a standing wave has been established there is no sign of a progressive wave in either direction and individual points on the cord are executing simple harmonic motions at right angles to the cord. The amplitude of this simple harmonic motion is greatest at equally spaced points which are called antinodes and zero at an equally spaced set of points which are called nodes. The two ends are always nodes and the length of the cord is a whole number of half wavelengths.
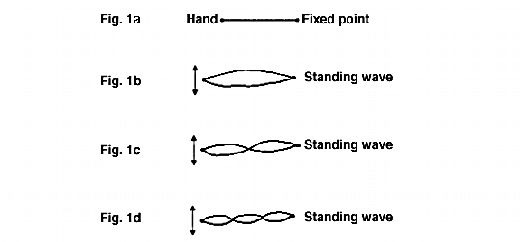
38. When infrared radiation is incident normally on a surface the theory of electromagnetism predicts that there will be a node at the surface and this was verified experimentally by Wiener as long ago as 1890. Hence, the electromagnetic wave will have zero amplitude at the surface, so that the absorption will be very small. It may also be shown that for non-normal incidence there is no longer a node on the surface and absorption will occur. It is therefore necessary to use non-normal incidence for this type of measurement. If the film is very thin, near-grazing incidence will give maximum penetration of the sample, and surface reflection is then also at a maximum.
The thin films examined at grazing incidence fall into two categories: they may be of the type where the metal substrate simply acts as a support. Alternatively, there may be adsorption on to the surface, so that interaction forces between the sample and the substrate come into play. In this latter case, an additional factor influences the spectrum. The molecular vibrations of the adsorbed molecules which occur in directions such that the resulting dipole moment changes lie parallel to the surface give no absorption, whereas dipole moment changes perpendicular to the surface give absorption peaks of maximum intensity. For this reason measurements with polarised radiation may prove advantageous. However, this is a specialist area of activity and it does not warrant detailed discussion in this general and introductory account.
REF: Int. J. Vib. Spect., [www.irdg.org/ijvs] 1, 5, 31-38 (1998)
