The Background to Sample Preparation for Infrared Transmission Measurements on Solids
William Maddams, University of Southampton
Until recently Chief Vibrational Spectroscopist, BP Research, Sunbury on Thames, UK.
Measurement of the transmission infrared spectra of liquids poses no great problem from the sampling viewpoint. These materials may be squeezed between polished plates of sodium chloride, potassium bromide, or another suitably transparent material until absorption bands of measurable intensity are obtained. The thickness of such films is usually a few microns. Alternatively, if information of a quantitative or semi-quantitative nature is required the sample is made up in solution, at 5 or 10% concentration, in a solvent such as cyclohexane, carbon tetrachloride, chloroform or carbon disulphide and examined in a sealed cell whose path length is, typically, 100 ?. Solids may also be examined in solution, given that a reasonably transparent infrared solvent can be found. It is also possible in some cases to cast thin films, a technique that is somewhat time consuming but is useful for some polymers.
However, when these approaches are not applicable because of sample insolubility and it is necessary to examine samples in powder form, problems arise for three reasons. Two of these relate to the particle size of the solid, in quite different contexts, and the third to the effect of sample refractive index. It is useful to have a basic understanding of why these problems occur and how their effects may be minimised in order to obtain good quality transmission spectra from solid samples.
1. Particle Size and Optimum Packing
It is a simple process to squeeze a liquid, however viscous, between optical flats and hence to make an acceptable thin layer. In contrast, the preparation of a continuous, homogeneous layer from a powdered solid poses considerable difficulties, not merely because the squeezing process is ineffective.
The problem may be understood by considering two model systems where the particles consist of (i) regular spheres and (ii) regular cubes. Fig.1a shows a cross-section of a group of regularly packed spheres of equal diameter. It is clear that there is considerable space between the spheres. Hence, if a collection of spherical particles of equal size is inserted into the beam of a spectrometer, a significant proportion of the radiation will not traverse the sample. If, as shown in Fig.1b, there is more than one layer of particles, it is possible for these to be arranged so that some of the gaps are closed. Alternatively, if the spherical particles cover a range of diameters, there is even less free space between them, as shown in Fig.1c. Again, multiple layers reduce still further the free space. However, the multilayer option is limited in practice; unless the particle size is below about one micron it will not be possible to achieve the optimum sample thickness we need – a few microns.
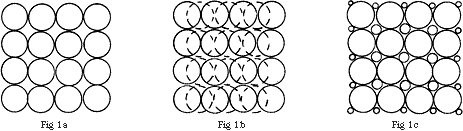
Figure 1
In the case of cubic particles, these may pack wholly regularly if they are of equal size, as shown in Fig.2a, and there is then no free space. However, if the packing is irregular as in Fig.2b, there will be some and this is likely to be rather greater if the cubic particles are not of equal sizes.
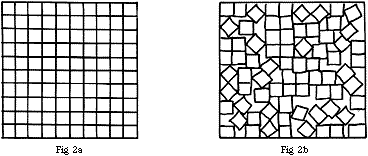
Figure 2
In practice, real particles are likely to be of irregular and varying size and shape and the presence of some free space is almost inevitable. What are the consequences?
Suppose that the free space amounts to 10% of the area over the cross-section of the spectrometer beam at the point where it traverses the sample. Then, if the sample is absorbing all of the radiation falling upon it, the measured absorbance will be log10 100/0+10, i.e. 1.0 instead of log10 100/0, i.e. 00. Similarly, if the sample absorbs 90% of the incident radiation the measured absorbance will be log10 100/10+10 = 0.70, rather than log10 100/10 = 1.0.
For a sample absorbing 60% of the incident radiation, the measured absorbance will be log10 100/40+10, i.e. 0.30 instead of the correct value of log10 100/40, i.e. 0.40. So the spectrometer will always give absorbance values that are too low and the error will be greater the greater the absorbance being measured.
2. Particle Size and the Reflection and Scattering of Radiation
If we consider a beam of light moving in a particular direction as a travelling sinusoidal wave, we would expect secondary wavelets to radiate from all points along that line. This does not happen in empty space because, as Fresnel showed many many years ago, there is destructive interference of the secondary wavelets that arise at all points traversed by the beam. However, in practice, secondary wavelets are generated at disturbances such as when the beam encounters a discontinuity of any sort, and these do not interfere destructively. A fraction of the light is then scattered over all angles around the beam and this scatter is dependent upon the size of the discontinuity, the wavelength of the light and the refractive index of the medium through which it is passing.
In the present context the discontinuity is the particle of our solid sample upon which the beam of infrared radiation falls and it is convenient to consider the matter in somewhat more detail. For practical purposes we will look at three groups of particle sizes. They are: particles of a size appreciably greater than the wavelength of the radiation, particles whose dimensions are comparable with ?, and particles appreciably smaller than ?.
(a) Particle size greater than ?
Imagine a cubic crystal, whose dimensions are appreciably greater than ?, sited so that one of its faces is perpendicular to the beam of radiation passing through the spectrometer. Most of the radiation will pass into the crystal, some will be absorbed, and the remainder transmitted. However, a fraction of it will be reflected from the surface of the crystal and be lost. The size of this fraction is determined by the difference in refractive index between the crystal and the surrounding medium (which, in the case of air, is a very close approximation to 1.0). If the crystal has a refractive index of 1.5, a figure fairly representative of many organic compounds, the loss amounts to 4%. For diamond, which has a refractive index of 2.4, the value rises to 17% and this is responsible for the glitter and sparkle. The overall reflectivity of a girl’s best friend is enhanced by cutting the diamond; the various facets reflect light at a range of angles and enhance the lustre and sparkle. This multiple reflectivity also occurs with a powder consisting of the cubic crystals considered above. Their faces will tend to be disposed randomly with respect to the beam of radiation. Since the reflection will take place specularly, the reflected radiation will leave the crystalline sample over a wide range of angles. There will be a substantial loss by scattering and this will occur for all types of crystals, irrespective of their symmetry. This reflection/scattering loss occurs for all particle sizes until they approach the wavelength of the radiation incident upon them. However, the smaller the refractive index difference between the particles and the surrounding medium, the smaller will be the radiation loss.
(b) Particle size comparable with ?
The scattering process is more complex in this instance because diffraction effects also occur, and the intensity of scattering is considerably larger. Rather than struggle with the theory, let me explain a demonstration of the effect where the particle size is comparable to visible light wavelengths.
One of the most convincing of these involves small particles of sulphur. If a very dilute solution of sodium thiosulphate is acidified with a few drops of dilute sulphuric acid, the sulphur that is formed in the ensuing chemical reaction precipitates very slowly as small particles that gradually increase in size. When they reach about 0.4 to 0.5 ? in size, the reaction mixture appears blue, because of the strong scattering of blue-green light.
When the particles have almost doubled their size they scatter red light but rather less strongly, the latter because of the wavelength dependence factor in the equation for the scattering intensity.
It is clear therefore that it is highly desirable that solid samples for examination by infrared spectroscopy should not contain a significant proportion of particles whose sizes are comparable to the wavelength range of the spectrum to be measured. In analytical infrared spectroscopy the wavelength range is huge, 2.75-25 microns, so we have to be careful. Fortunately, there is normally no great difficulty in reducing the average particle size below 2.75 ? so that, on this count, the problem is much reduced. There is, however, another factor which produces scattering when the particle size is below ? and this will be considered below.
(c) Particle size smaller than ?
This type of scattering was studied in detail, both theoretically and experimentally, by Lord Rayleigh a century and a quarter ago. He showed that the scattering intensity is proportional to the sixth power of the particle diameter and inversely proportional to the fourth power of the wavelength (this latter also being the case for Raman scattering). These two terms tend to operate in opposite directions but, in practice, the diameter term is much the more important because the lower limit on ? is set by the wavelengths of the various vibrational frequencies we want to measure. There is also a practical limit to the fineness that may be achieved by intensive grinding; in many cases once the particle size falls appreciably below about 1? the particles start to stick together as the result of surface forces and behave optically as rather larger ones.
Rayleigh type scattering, as it is usually called, can occur with small molecules. Lord Rayleigh showed that the blue colour of the sky is the result of scattering by the oxygen and nitrogen molecules of the air. Although the scattering intensity from an individual molecule is very small, the thickness of the earth’s atmosphere leads to a colouration readily detectable by the human eye. All transparent dust-free liquids show Rayleigh scattering. Logically, the scattering intensity for a liquid must be much stronger than for a gas. After all, there are about 1000 times more molecules per unit volume in a liquid than there are in a gas at one atmosphere pressure! In practice the intensity comparison is not 1000:1 but much less, at around Intensity liquid/Intensity gas = 50.
This apparent anomaly is nothing of the sort, since it is in agreement with theoretical predictions. Liquids are much closer to continuous media than gases so, as we saw above, Fresnel would point out that the secondary wavelets in liquids will tend to destructively interfere. Now, if our solid were to be surrounded by a liquid of the same refractive index, it too would approach continuity and as a result the scattering would be much less than it would be from a dry powder. That this is so is easily demonstrated. If a glass rod is dipped into Canada balsam or oil of cedar, it becomes practically invisible (The lads who repair stone damage to car windscreens use this principle). We exploit this effect in preparing solids for infrared analysis – grind the powder to a particle size smaller than the shortest wavelength we plan to use and immerse the analyte in a fluid of matching index of refraction.
3. Practical Methods
So, we plan to coat the particles of a solid sample, preferably reduced in size to about 1 ?, with a transparent liquid of comparable refractive index. How may this be done in practice? Apart from meeting the refractive index criterion, the liquid of choice must be as transparent as possible over the range 2.75-25 ?. Inevitably, compromise is necessary, as is the case with solvents used for solution studies. Paraffinic hydrocarbons provide one such compromise, although they absorb rather strongly at the frequencies specific for the various types of C-H vibrations.
A high molecular weight paraffinic hydrocarbon is desirable because it will have a low volatility, a higher refractive index than the lighter paraffins, and a usefully high viscosity, thereby aiding the coating process. Medicinal liquid paraffin has been used for this purpose since the early days of analytical infrared, and the technique is universally known as the Nujol mull. Why Nujol? Many years ago a proprietary brand of constipation curer named NUJOL was widely available in pharmacies. It transpired that NUJOL was the best and most reliable source of liquid paraffin – as simple as that. Some skill and experience are required to produce good mulls consistently. It is not much of a problem to get the correct particle size of the solid but it is tricky to get the right proportions of Nujol and solid for a stiff, homogeneous paste, without excess liquid. Nevertheless, this approach has been used with great success for more than half a century.
Since the wetting fluid has its own spectrum there is an interference problem. It is tempting to use the computer to subtract the spectrum of the Nujol from that of the mull and a lot of people do just this, but it is really bad practice. Since your subtraction can never be perfect, you will never be certain that what you are left with is meaningful. You MUST make a mull with a material that does not interfere and then merge the data. In Fig.3 you will see the infrared spectra of Nujol and an alternative mulling fluid, in this case hexachlorobutadine. Now, hexachlorobutadine H.B. is a relatively oily material of high index which has an intense infrared spectrum of its own but it contains only C-C and C-CL bonds. As a result, it does not absorb between 1250 and 1500 cm-1 or above 2000 cm-1 so it does not interfere where Nujol does. The problem with H.B. is that it is poisonous, so these days fluorocarbon oils have become popular.
Predictably, mulls provide an essentially qualitative approach. Nevertheless, they have been used to a limited degree for quantitative work, by incorporating an internal standard such as potassium thiocyanate, and utilising the characteristic peak in the vicinity of 2050 cm-1 as an intensity marker. There are problems associated with the reproducible grinding of both solids and the subsequent mixing but, with care, successful analyses are possible.
Liquids provide a reasonable approach to a continuous medium but some solids are even more perfect in this respect, and good quality of crystals such as quartz scatter less light than transparent liquids. In these crystals the molecules are arranged in a regular manner and this condition approaches that of a continuous medium from a mathematical standpoint. Hence, the destruction of secondary wavelets, as envisaged by Fresnel, is virtually complete. However, is it possible to disperse fine particulate samples uniformly in a homogeneous optically transparent solid? The answer is of course yes and it proves to be easier than might be envisaged.
The alkali halides, such as sodium chloride and potassium bromide, all have simple cubic structures. Cleavage along planes parallel to the crystal faces (and possibly along diagonal faces) should, in principle, be possible by the application of force. The ease of cleavage is determined by the surface energy of the crystal, and this may be calculated theoretically. The values so obtained are rather high but in practice it is found that the cleavage energies are two orders of magnitude smaller than expected. This considerable discrepancy probably arises from lattice imperfections, such as tiny surface cracks, which initiate cleavage. However, what is important for our purpose is that conventional laboratory grinding methods reduce the alkali halides to microcrystalline particles.
Because the cohesive energy is relatively low such powders, if subjected to a pressure readily attainable in a modest laboratory press, reform into clear homogeneous solids, a process often referred to as “cold sintering”. The pressure required for the process is lowest for potassium bromide, followed by potassium chloride. If, therefore, an appropriate concentration of the solid whose spectrum is required, with a particle size of about 1 ?, is dispersed into potassium bromide powder and pressed, a clear transparent disc is obtained, ready for insertion into the spectrometer. Since the alkali halides transmit infrared well except at long wavelengths, we do not have the interference problem typical of mulls, but remember – the particles of solid must be as fine as they are in a mull and the concentration of the analyte and its thickness must be just right to record a good spectrum.
The practical details of this process have been discussed above in depth by Dr. G. Dent and do not require amplification. Two points of detail do merit comment. The thickness of the alkali halide disc is set primarily by its mechanical strength, and the weight of potassium bromide powder for a 13 mm die recommended by Dr. Dent will ensure that discs do not fracture during handling. With this thickness of disc, a sample concentration in the range 0.5% to 1.0% usually gives peaks of optimum intensity. It may be noted, in passing, that discs may also be prepared using caesium halides, particularly caesium iodide. This is transparent as far as 180 cm-1, whereas the cut-off for KBr is about 300 cm-1. Discs may also be prepared from very finely powdered polyethylene, and these extend the working range still further into the far infrared region.
Dr. Dent refers, in passing, to the distorted bandshapes that may occur because of what is known as the Christiansen effect, and it is useful to briefly consider the background to this.
In the case of a material such as potassium bromide, which is transparent over the mid-infrared range of, say, 2.5 ? to 25 ?, the refractive index decreases slowly with increasing wavelength. However, the situation is very different with a material having vibrational frequencies in this range. As an absorption band is approached from the high frequency side, the refractive index falls. Moving to the low frequency side of the vibrational frequency, the refractive index is anomalously high and then drops back to the value expected in the absence of an absorption. It may be noted that this effect also occurs strongly with electronic absorption bands and it was in this field that Christiansen did his pioneering work. This change in the refractive index distorts the shape of the absorption peaks in infrared spectra. In some cases the distortion is so marked that the short wavelength side of the peak may appear to be negative, giving it the appearance of a first derivative spectrum. This effect disappears when the particle size is smaller than ?; hence, it should not appear if the sample preparation has been done properly. Some hard materials may be difficult to grind down to the required average particle size but fortunately they are in the minority.
One final point; the Christiansen effect applies in both alkali halide discs and in mulls.
A useful source on this subject is “Laboratory methods in Vibrational Spectroscopy”, Ed. Willis, Van der Maas and Miller.
REF: Int. J. Vib. Spect., [www.irdg.org/ijvs] 1, 1, 3 (1996)
