An Attenuated Total Reflection Infrared Spectroscopy of Water Solutions
Joze Grdadolnik
National Institute of Chemistry,
Hajdrihova 19, SI-1000 Ljubljana,
Slovenia
E-mail:joze.grdadolnik [at] ki.si
Abstract
In this article the main advantages and limitations of the ATR* technique are presented. As examples, the ATR spectra of liquid phase water and a water solution of bovine serum albumin are used. The main differences between the transmission infrared spectroscopy and ATR are pointed out. Also shown is the optical constant method of calculation, using the CIRCLE™ ATR liquid cell, and from optical constants the calculation of the dielectric constants e‘ and e”. The pure absorbance spectrum is calculated and shown to be fully comparable with transmission spectra.
* Abbreviations: ATR attenuated total reflection,
IRE internal reflection element,
FTIR Fourier transform infrared,
IR infrared,
K-K Kramers-Krönig transformation,
BSA bovine serum albumin
™CIRCLE is trademark of Thermo Spectra-Tech.
Introduction
Transmission FTIR spectroscopy is the IR method most commonly used in biophysical studies. However, there are a number of technical difficulties commonly encountered with this technique that can make collection of high quality spectra difficult. These difficulties are usually expressed using liquid samples. In the transmission technique the angle of incidence of the radiation at the cell is a narrow cone around normal. This is ideal, but the reproducibility of the path length is hard to guarantee. This is of overwhelming importance when a solvent such as water is used. Water is an extremely strong absorber (molar absorptivity 104.4 M-1cm-1 near 3 m m wavelength) a characteristic it shares with most compounds containing OH groups and often leads to signal saturation. The smallest commercially available cell spacers, which are 6 m m thick, produce an absorbance near 3 absorbance units, where a linearity of all commercial known detectors is corrupted. In other words, the region between 2800 cm-1 and 3700 cm-1 is void of useful information. Furthermore, bands in this region, are fully overlapped with usually much broader and intense OH stretching modes and hence are lost for further exploitation. Because of a non-linear detector response the subtraction is useless. Therefore, the spacer thickness should be reduced to avoid saturation effects. This typically needs to be below 1 mm for dilute water solutions. However, using such thin spacers causes problems with reproducibility. Further, it is not trivial to fill such liquid cells because air bubbles become incorporated in the sample. Concomitant with reducing the spacer thickness, we also approach the limit where the effects of the surface water are not negligible, i.e. the perturbation of surface water molecules (or other solvent used) by the window material may become important, and may significantly alter the spectrum of the “bulk sample”.
An alternative solution to the experimental problem is to use attenuated total reflection (ATR) [1, 2]. In this method a solid or liquid sample must be brought into contact with an optical element wherein the light is totally internally reflected and where the sample interacts with the evanescent wave. The effective path length for this interaction depends on several parameters and is typically a fraction of a wavelength [Editor’s Note: ATR has been discussed in IJVS – seeEdition 2 of Volume 2]. Because of the small light penetration depth, the ATR technique is ideal for highly absorbing samples and for surfaces and thin film measurements. Generally, the ATR spectra are similar to regular transmission; however, for thick samples when spectra are recorded at angles greater than critical, the wavelength dependence is observed. Penetration depth dp is hence equal to
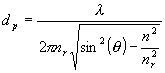 (1)
(1)
where λ is vacuum wavelength of the radiation, nr and n are the real refractive indices of the prism optical material (the IRE) and sample, respectively, and θ is the angle of incidence. Moreover, ATR spectra possess not only the absorption features, but also reflection components. Therefore ATR spectra can not be used in a quantitative manner (band shape analysis, determination of oscillator strengths ,…) directly. To obtain the absorption spectrum, we have to separate both contributions, i.e. the optical constants n and k must be calculated. After this operation, spectra recorded in the normal transmission mode can be fully comparable to those recorded in the ATR setup. The optical constants of materials can be precisely determined by combining measurements made at different angles of incidence. Most commercial ATR cells do not have the ability to change the incident angle. Hence to calculate the optical constants, an alternative procedure called the Kramers-Kronig (K-K) method has to be used [3-5]. This method is based on the interdependence of the optical constants and on the use of Fresnel’s equations.
In this paper the main differences between absorption and ATR spectra will be discussed. These differences will be presented in two examples, i.e. liquid water and dilute protein (bovine serum albumin, BSA) in phosphate buffer. We used these two systems first to demonstrate the differences between the experimental ATR spectra and calculated spectra and second to present the method of calculating the absorption spectrum from the reflection spectrum. Since, the widely acknowledged ![]() effect on ATR absorbance, which is usually described as the ATR correction in commercial software, is not the only distortion in ATR spectra, the influence of the so called anomalous dispersion must be taken into account.
effect on ATR absorbance, which is usually described as the ATR correction in commercial software, is not the only distortion in ATR spectra, the influence of the so called anomalous dispersion must be taken into account.
Background
Since the optical constants are known, it is very easy to calculate both real (n) and imaginary (k) dielectric constants and absorption spectra (A). From a known k, the absorption spectrum can be expressed using equation (1), where ![]() represents frequency in cm-1 and det effective sample thickness in cm as follows:
represents frequency in cm-1 and det effective sample thickness in cm as follows:
![]() (2)
(2)
Equations (2) and (3) connect both dielectric constants ![]() with optical constants (
with optical constants (![]() ):
):
![]() , (3a)
, (3a) ![]() (3b)
(3b) ![]() (3c)
(3c)
Optical constants can be calculated using K-K transformation, which yields ![]() from
from ![]() and vice versa.
and vice versa.
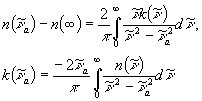 (4)
(4)
In general K-K transformation connects several frequency dependent imaginary and real physical quantities with integral equations. Hence instead of using n and k the reflectivity Rs and phase angle θ s can also be used [6].
The reflectivity at the interface between a non absorbing medium of refractive index nr and absorbing medium of refractive index n and dielectric constants given by the equations (2) and (3) for parallel polarized light is
![]() (5)
(5)
where
![]()
![]() and
and ![]()
(6a) (6b) (6c)
For detailed analyses and comparison between the calculated reflectivity (Rs) and the experimental spectrum (ATR), we have to know their mutual dependence [3]
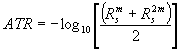 (7)
(7)
with the solution for Rs as
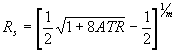 (8)
(8)
Equation (8) is written for the geometry of CIRCLETM cell only (Figure 1b), where θ is 45° and where reflectivity in both polarizations are related as Rp=Rs2. This relation is used during the iterative procedure of calculating the n and k by K-K transformation when the calculated values are compared with the original spectrum. In general, the system of Fresnel equations must be solved for the given optical system to get the relation between the spectrum and reflectivity.
Results and discussion
Two typical ATR experiments are shown in Figure 1. The first one represents a horizontal ATR plate covered with a sample. All kinds of samples can be measured using a horizontal ATR cell, from solids through pastes to liquids. The only limitation is, as in all ATR experiments, that we have to ensure precise contact between the sample and the IRE i.e. the sample must ‘wet’ the IRE. Usually it is easy to fulfill this condition, especially when liquid samples or deposited films build up directly on the IRE are used. Difficulties may arise with solid samples. There are two possibilities for overcoming problems with the contact area when solid samples are used. First a clamp may be used to ensure optical contact, so-called a mouse-trap, i.e. a solid cover where the pressure of the sample on IRE can be precisely regulated. With constant pressure the reproducibility of ATR spectra is fulfilled. Alternatively, use of a Nujol (similar as in the transmittance experiment), which serve as a matrix to allow better contact between the solid sample and IRE.
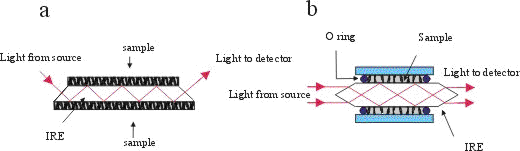
Figure 1. (a) A horizontal geometry ATR cell and
(b) CIRCLETM ATR cell for liquid samples.
For liquids, a specially designed CIRCLETM ATR cell can be used. Besides its simple geometry, its main advantage is that it guarantees very effective contact between the sample and IRE. It possesses a very high degree of symmetry, and hence makes calculation of optical constants easier. In this article all measurements and consequently calculations are made using this type of ATR cell. Several types of material with high refractive indices for IRE are used in both types of cells. Most frequently used are ZnSe (nr=2.4 at 1000 cm-1), AMTIR (GeAsSe glass , nr=2.5 at 1000 cm-1), Si (nr=3.4 at 1000 cm-1) and Ge (nr=4.0 at 1000 cm-1). For a given wavelength, the dp is determined by the refractive index of the IRE according to equation (1).
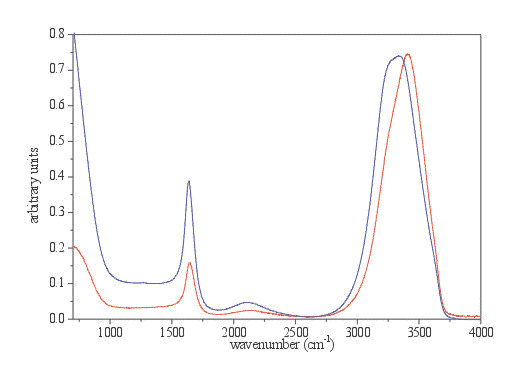
Figure 2. The spectrum of liquid water recorded with a 2 m m thick normal liquid cell with ZnSe windows in transmission mode (red spectrum) and original ATR spectrum (blue spectrum) both normalized to the OH stretching intensity.
| ? OH | d OH | |
| transmission | 3407 | 1644 |
| original ATR | 3337 | 1636 |
| corrected ATR | 3336 | 1635 |
| calculated absorbance | 3406 | 1644 |
Table 1. Band frequencies of stretching and bending mode of liquid water for various types of spectra (in cm-1).
A spectrum of liquid water is a very illustrative example of the distortions in band shape and frequency due to anomalous dispersion. Details are presented in Figures 3 and 4 and in Table 1. The main distortion can be observed in the region of OH stretching. The band maximum is shifted to lower frequency for 70 cm-1. The changes in the OH bending region are less pronounced, except the change in relative intensity. With the ATR correction, which is usually included in commercial software, only the adjustment for the wavelength dependance of penetration depth is taken into account. The effects of this calculation are presented in Figure 5. These calculations (using equation 1) adjust the relative intensity in the whole spectrum region to normalise them with the transmission spectrum. However it does not alter the band shapes, which remain almost the same.
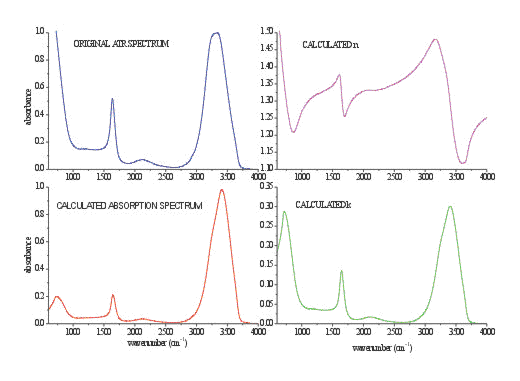
Figure 3. Calculated n (purple spectrum) and k (green spectrum) of pure water from the spectrum shown in Fig.2. Values of both optical constants are the same as previously calculated in Refs.. For comparison the original ATR spectrum (blue spectrum) and calculated (red spectrum) are shown.
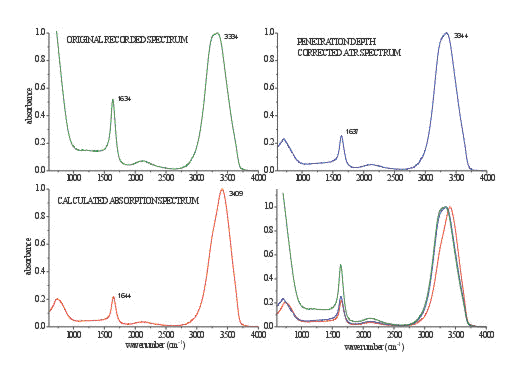
Figure 4. An ATR spectrum of liquid water (green spectrum), corrected ATR spectrum using commercial software (blue spectrum), calculated spectrum from optical constants (red spectrum) and direct comparison of all presented spectra
To obtain a spectrum, which is also comparable in bandshape with the spectrum from the transmission measurement, the optical constants n and k must be calculated first. Figure 3 illustrates both constants, calculated with the K-K transformation for optical system in the CIRCLETM cell. Once n and k are known, it is trivial to calculate the absorbance spectrum using equation 1 or dielectric constants calculated from equations 3a and 3b.
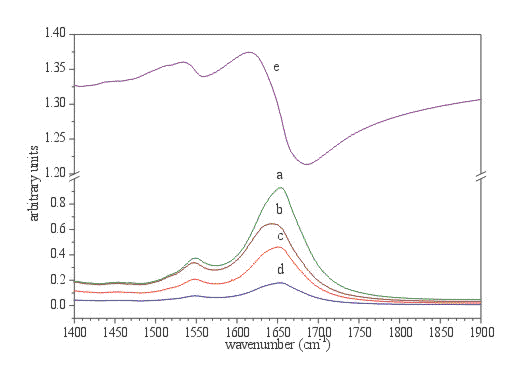
Figure 5. Amide I and Amide II region of protein spectrum (BSA, 2.4 mM solution in phosphate buffer, ATR CIRCLE cell) after subtraction of phosphate buffer. a. calculated absorption spectrum d=0.5mm, b. original ATR spectrum, c. calculated imaginary part (e”) of ![]() , d. calculated k, and e. calculated n.
, d. calculated k, and e. calculated n.
Another illustrative example of the band distortion using the ATR technique comes from the spectra of protein in buffer solutions [9,10]. It is well known that from the IR spectra of proteins, the secondary structure of proteins can be determined. Especially useful is the Amide I band, which is, in the case of folded proteins, composed of several bands, which belong to different classes of secondary structure elements. These bands are usually evaluated with a band fitting algorithm and/or Fourier self deconvolution [11,12]; the frequency of the components determines the type of secondary structure (a helix, ß sheet and various types of turns), while the area of these bands is connected to the population of secondary elements in the protein molecule [13,14]. Hence, for precise structural determination, the exact knowledge of the shape as well as the frequency of the Amide I band is a requirement. From Figure 6 it is obvious that anomalous dispersion of real refractive index n has dramatic effects on the shape, as well as on the frequency, of both Amide I and Amide II bands. It can be noticed without the use of resolution enhancement techniques such as second derivative spectroscopy and Fourier deconvolution, that decomposition of both Amide I bands would yield completely different results. It has to be emphasized that among the band mechanisms of distortion mentioned, the solvent subtraction (in our case phosphate buffer) can also disrupt the structure of the Amide I band. Namely the -OH bending mode at 1640 cm-1 is strongly overlapped with Amide I band. Only the bulk phosphate buffer can be successfully subtracted, and is not effected by the presence of the protein molecules. The differences in the shape and frequencies can also be observed in the Amide II region and in the high frequency region of the Amide I band, i.e. the regions which are not disturbed by the overlapping of the -OH bending mode. From the difference spectrum, presented in Figure 6, the band distortions in the ATR spectrum can be estimated.
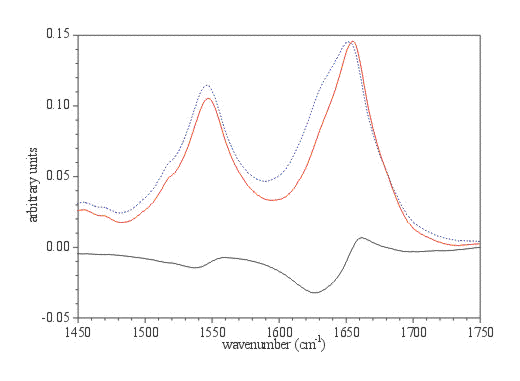
Figure 6. The Amide I and II regions of BSA in the original ATR spectrum (dashed blue spectrum) and calculated absorption spectrum (red spectrum). Phosphate buffer is subtracted and original ATR spectrum is corrected for wavelength dependence of the depth of light penetration using commercial ATR correction (Eq. 1). The bottom spectrum represents the difference between upper ones.
The band area of the Amide I in ATR spectrum, previously corrected for the wavelength dependence of light penetration into the sample, is roughly 10 to 15% larger than in the calculated one. Since the secondary structure determination of proteins using IR spectra can be calculated with a relative error smaller that 5%, these refraction distortions are a source of concern in structure determination. This problem, as it was demonstrated, can be simply overcome with the calculation of optical constants.
Conclusions
Transmission techniques are still widely used in routine as well as in research FTIR spectroscopy. In addition to their simplicity and universal use, the frequencies of bands and the band shape are directly related to microscopic physical quantities and hence the spectra can be interpreted without any correction. However, the development of FTIR accessories their application in research areas of biological significance enable us to apply FTIR to systems of interest where water is the most important solvent. Water solutions and water itself have been for many years been unattractive in infrared spectroscopy, and only since the application of ATR techniques can useful spectra can be recorded. With this technique a mid-infrared spectrum can used without any restrictions due to saturation effects of the OH bands. The only drawback is that the ATR spectra need further processing in order to get physical significance on a molecular level. This can be easily achieved with the calculation of optical constants using well-known K-K transformations. From the two examples described in this paper it can be deduced that calculation of optical constants is mandatory when an ATR experiment is used. Although there are some minor anomalies in the calculation of optical constants using the K-K transformation (spectrum is measured in a finite interval, usually only approximate value of ![]() is known, imperfections of optical instrumentation), the similarity between the spectra calculated from the optical constants and the spectra measured in transmission technique is better than 10-3absorbance units. This improves further if we are able to mathematically describe and/or avoid some of the difficulties in the procedure of calculating the optical constants. This is also one of the reasons why the CIRCLETM cell is so widely used. Its high symmetry and simple but highly refined optics are characteristics, which allow us to calculate a spectrum even more accurately. A methodology of calculating n and k for CIRCLE and horizontal ATR (both optical path are presented in Figure 1) will be evaluated and described in a forthcoming paper.
is known, imperfections of optical instrumentation), the similarity between the spectra calculated from the optical constants and the spectra measured in transmission technique is better than 10-3absorbance units. This improves further if we are able to mathematically describe and/or avoid some of the difficulties in the procedure of calculating the optical constants. This is also one of the reasons why the CIRCLETM cell is so widely used. Its high symmetry and simple but highly refined optics are characteristics, which allow us to calculate a spectrum even more accurately. A methodology of calculating n and k for CIRCLE and horizontal ATR (both optical path are presented in Figure 1) will be evaluated and described in a forthcoming paper.
Acknowledgements
This work was supported by the Ministry of Science and Technology of the Republic of Slovenia. Part of this work was done at CEA/PCM/DRFMC Grenoble, France, and contribution to this study by the Commisariat à l’Energie Atomique in the form of a grant is greatly acknowledge. The author is grateful to Prof. Yves Maréchal for many stimulating discussions and to the referee for useful comments and suggestions.
References
- J. Fahrenfort, Spectrochimica Acta, 17, 698 (1961).
- N.J. Harrick, Internal Reflection Spectroscopy, Interscience Publisher, New York, London, Sydney, 1967.
- J.E. Bertie & H.H. Eysel, App. Spec., 39, 392-401 (1985).
- J.E. Bertie, M.K. Ahmed & H.H. Eysel, J. Phys. Chem., 93, 2210-2218 (1989).
- J.E. Bertie & S.L. Zhang, Can. J. Chem., 70, 520-531 (1996).
- J.E. Bertie & Z. Lan, J. CHem. Phys., 105, 8502-8514 (1996)
- U. Kuenzelmann, H. Neugebauer & A. Neckel, Langmuir, 10, 2444-2449 (1994).
- Y. Maréchal, J. Chem. Phys., 95, (1991).
- J. Grdadolnik & Y. Maréchal, Biopolymers, 62, 54-67 (2001).
- J. Grdadolnik & Y. Maréchal, Biopolymers, 62, 40-53 (2001).
- H.H. Mantsch, H.L. Casal & R.N. Jones. In Advances in Spectroscopy, Eds.,
- R.J. Clark & R.E. Hester, John Wiley & Sons, Chichester, New York, Toronto, Singapore, (1986) Vol 13, pp 1-42.
- J.K. Kaupinnen, D.J. Moffatt, H.H. Mantsch & D.G. Cameron, App. Spec., 35, 1454 (1981).
- S. Krimm, J. Mol. Biol., 4, 528-540 (1962).
- S. Krimm & J. Bandekar, Adv. Prot. Chem., 38, 181-264 (1986).
Received 23rd January 2002, accepted 5th March 2002.
REF: J. Grdadolnik, Int. J. Vib. Spect., [www.irdg.org/ijvs] 6, 2, 6 (2002)

